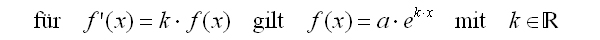|
|
|
| Seite 1 |
Seite 2 |
Seite 3 |
|
|
| Wachstums- und Zerfallsfunktionen |
|
| Besonders bei Wachstums- und Zerfallsprozessen spielen e- und ln-Funktionen eine große Rolle. Sie sind dabei eine Lösung der Differentialgleichung |
|
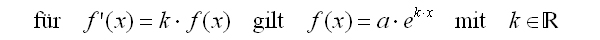 |
|
| Die Konstante k heißt Wachstums- oder Zerfallskonstante. Wachstums- und Zerfallsfunktionen beginnen zum Zeitpunkt x = 0. |
|
| Aufgabe: |
|
|
|
|
| 1)
| |
Betrachten Sie zunächst B(x). Verändern Sie die Werte für a1 und k1. Für welche Werte von k liegt ein Wachstum vor, für welche ein Zerfall? Welche Funktion hat a? |
|
| 2)
| |
Eine im reellen Bezug oft verwendete Bezeichnung ist die Verdoppelungs- bzw. Halbwertszeit, also die Zeit, in der sich ein Bestand verdoppelt bzw. halbiert. Berechnen Sie diese und überprüfen Sie das Ergebnis für mehrere Einstellungen von a und k mit Hilfe des Schnittpunktes mit der Geraden x = t. |
|
| 3)
| |
Eine andere Art des Wachstums ist das beschränkte Wachstum. Natürliche Wachstumsvorgänge verlaufen meist nur zu Beginn exponentiell und nähern sich dann einer natürlichen Grenze. Betrachten Sie nun W(x) und klären Sie durch verschiedene Einstellungen von a2, k2 und G, welche Funktion diese Parameter haben. |
|
| 4)
| |
Finden Sie Beispiele aus der Natur, die ein beschränktes Wachstum beschreiben und erklären Sie, warum es zu einer solchen Beschränkung kommt. |
|
|
|
|
| Seite 1 |
Seite 2 |
Seite 3 |
|
|
|
|