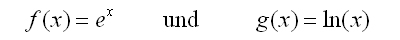|
|
|
| Seite 1 |
Seite 2 |
Seite 3 |
|
|
| Natürliche Exponential- und Logarithmusfunktion |
|
| Da Sie bereits in JgSt. 10 die Exponential- und Logarithmusfunktion kennen gelernt haben, sind sowohl die natürliche Exponential- als auch die natürliche Logarithmusfunktion keine wirklichen Neuerungen mehr. Ihre Funktionsgleichungen lauten: |
|
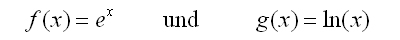 |
|
| Die Basis der natürlichen Exponentialfunktion, oder einfach e-Funktion bzw. exp(x), ist die Eulersche Zahl e = 2,71828... . |
|
| Aufgabe: |
|
|
|
|
| 1)
| |
Ändern Sie mit Hilfe des Schiebereglers die Werte der Parameter a, b und c und beschreiben Sie den Verlauf des Schaubildes unter Berücksichtigung der Parameter. |
|
| 2)
| |
Leiten Sie f für verschiedene Werte von a, b, und c ab und prüfen Sie Ihre Ableitungen, indem Sie in die Befehlszeile "Ableitung[f]" eingeben. Welche Ableitungsregel benötigen Sie beim Ableiten? Welche Parameter spielen für die Ableitung eine Rolle? |
|
| 3)
| |
Leiten Sie nun auch g ab und Zeichnen Sie g' ebenfalls ins Koordinatensystem ein. Was fällt Ihnen an g und g' auf? Betrachten Sie dabei besonders g als Integralfunktion von g'. |
|
|
|
|
| Seite 1 |
Seite 2 |
Seite 3 |
|
|
|
|