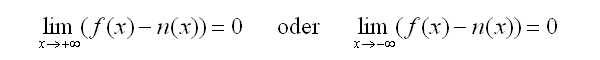| Seite 1 |
Seite 2 |
Seite 3 |
|
|
| Asymptoten, bzw. Näherungsfunktionen von gebrochen-rationalen Funktionen |
|
| Gibt es eine Funktion n(x), so dass |
|
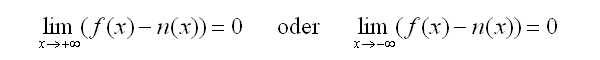 |
|
| gilt, so nennt man das Schaubild von n Asymptote des Schaubildes von f. n(x) wird als Näherungsfunktion bezeichnet. |
|
| Auf Seite 1 waren sowohl Zähler- als auch Nennergrad höchstens vom Grad 1. Wie aber die Anzahl und das Aussehen von Asymptoten vom Grad des Zähler- und Nennerpolynoms abhängen, soll folgende Aufgabe klären. |
|
| Aufgabe: |
|
|
|
|
| 1)
| |
Stellen Sie folgende Werte für die Parameter ein: a=0, b=0, c=1, d=0, p=1, q=0, r=-1. Bestimmen Sie mit obiger Formel n(x) und zeichnen Sie diese zur Überprüfung durch Eingabe von "n(x)=..." in die Befehlszeile ins Koordinatensystem ein. Notieren Sie Zähler- und Nennergrad sowie den Grad von n. Wie viele Polstellen gibt es? Notieren Sie auch diese Anzahl. (Dezimalzahlen werden mit "Punkt" eingegeben. Beispiel: 0.5) |
|
| 2)
| |
Stellen Sie folgende Werte für die Parameter ein: a=0, b=0, c=3, d=0, p=0, q=2, r=-4. Verfahren Sie dann wie in Aufgabe 1). |
|
| 3)
| |
Stellen Sie folgende Werte für die Parameter ein: a=0, b=2, c=1, d=0, p=0, q=2, r=-1. Verfahren Sie dann wie in Aufgabe 1). |
|
| 4)
| |
Stellen Sie folgende Werte für die Parameter ein: a=1, b=0, c=1, d=1, p=0, q=1, r=0. Verfahren Sie dann wie in Aufgabe 1). |
|
| 5)
| |
Können Sie nun eine Aussage über die Anzahl und die Art von Asymptoten bzw. Näherungsfunktionen in Abhängigkeit des Zähler- und Nennergrades machen? |
|
|
|
|
| Seite 1 |
Seite 2 |
Seite 3 |
|
|
|