Sätze

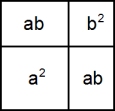
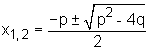In mathematischen Theorien werden  wichtige Einsichten als Sätze formuliert und bewiesen. In der Schulalgebra werden elementare Eigenschaften von Zahlen und Funktionen erarbeitet. Im Vordergrund stehen dabei Eigenschaften, die sich durch Gleichungen ausdrücken lassen. Auch in der Schulalgebra verdienen es einige Sachverhalte, als Sätze hervorgehoben zu werden. Dafür einige Beispiele:

Formeln

Satz: Für alle reellen Zahlen a,b gelten die binomischen Formeln:
(a + b)² = a² + 2ab + b²;   (a - b)² = a² - 2ab + b²;
(a + b)(a - b) = a² - b²

Funktionseigenschaften

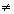Satz: Die quadratische Funktion mit f(x) = ax², a0,  ist gerade, d.h. für alle x gilt f(-x) = f(x). Das zeigt sich daran, dass ihr Graph symmetrisch zur y-Achse ist.

Existenzsätze

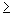Satz: Die quadratische Gleichung x² + px + q = 0 ist genau dann reell lösbar, wenn p² - 4q  0. Das erkennt man aus der Lösungsformel, denn genau dann ist die Wurzel reell.