Wir müssen also das Integral der Mantelfläche von
x= - r bis x = s berechnen.
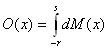
Die Berechnung vereinfacht sich, wenn man bedenkt, aus welchen Teilen die
Oberfläche zusammengesetzt ist. Ein Teil ist der einer Kugel und der andere ist
ein Körper, der entsteht, wenn man eine Parabel um ihre Symmetrieachse rotieren
lässt.
Der kugelförmige Teil ist die Oberfläche einer Kugel (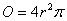 )
ohne die Oberfläche des fehlenden Segments ( )
ohne die Oberfläche des fehlenden Segments (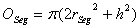 ).
In unserem Fall ist ).
In unserem Fall ist 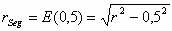 und und
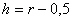 . .
Damit ergibt sich eine Oberfläche des Kugelstücks von
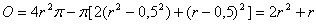
|