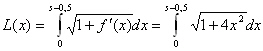Um die Oberfläche des Parabelstücks zu berechnen, wenden wir die Mittel der Analysis an. Wir zerlegen die Oberfläche in kleine Mantelflächen von Kegelstümpfen, für die gilt:
. r

Betrachten wir statt der Wurzelfunktion die Parabelfunktion. Diese verschieben wir wieder so im Koordinatensystem, dass ihr Scheitel im Ursprung liegt. Ihre Form und Länge ändert sich dabei nicht. Damit erfüllt sie die Gleichung

Zur Bestimmung der Oberfläche genügt es, die Länge der Kurve zu bestimmen, da beim Aufaddieren der kleinen Mantelflächen der Kegelstümpfe sich jeweils der kleine Radius des einen Mantels sich mit dem großen Radius des nächsten Mantels weg hebt, so dass am Ende nur noch der Radius an der Stelle x = 0,5 übrig bleibt.

Die Länge der Kurve bestimmt sich durch die Formel
Mit der Substitution 2 x = z und dx = 0,5 dz erhält man das Integral

und nach einsetzen der Grenzen ergibt sich die Länge der Kurve und durch Multiplikation mit und p(s-0,5) die gesuchte Oberfläche.