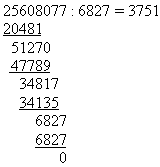Die Division mit den Neperschen Rechenstäben

Ein Beispiel:

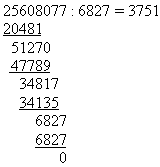Wie würde man auf herkömmliche Weise dividieren? Zunächst schaut man, wie oft 6827 in 25608 paßt (3 mal); nun rechnet man 3 mal 6827 und zieht dieses Ergebnis von 25608 ab (ergibt 5127);  die nächste Ziffer (0) wird heruntergeholt (ergibt 51270); nun schaut man wieder, wie oft 6827 in 51270 paßt usw.

Der entscheidende Vorteil beim Dividieren mit den Neperschen Rechenstäben liegt nun darin, daß man den jeweiligen Quotienten nicht durch Versuche ("wie oft paßt es?") herausfinden muß. Vielmehr werden die Produkte mit den möglichen Quotienten von 1 bis 9 bereits angezeigt, so daß man nur noch vergleichen muß.

Wie muß man beim obigen Beispiel 25608077 : 6827 vorgehen?

Als erstes legt man sich aus den Rechenstäben den Divisor 6827. Von oben nach unten werden nun also die Produkte 6827 mal 2, 6827 mal 3 usw. bis 6827 mal 9 angezeigt. Man schaut nun, welches dieser Produkte am besten in den ersten Divisor 25608 paßt. Man liest ab, daß 6827 mal 3 die Zahl 20481 ergibt, 6827 mal 4 aber schon 27308, also zu groß ist. Wir erhalten den ersten Quotienten 3. Aufschreiben kann man dies wie auf obige herkömmliche Weise; man spart sich eben nur das Ausprobieren. Nach Abzug des Produkts käme nun als nächstes 51270 (vgl. oben). Wir sehen, daß 6827 mal 7 47789 ergibt, 6827 mal 8 aber schon 54616. Folglich ist der zweite Divisor die 7, usw.