|
| Examensaufgaben - Erste Staatsprüfung für ein Lehramt an öffentlichen Schulen, Fachdidaktik Mathematik - Mittelschule (33910, 33911, 43918) |
| Examensaufgaben vor 1990 |
1989/II,1
1. Gegeben sind zwei sich schneidende Kreise K1 und K2 mit gleichgroßem Radius r (Mittelpunkte M1 und M2, Schnittpunkte A und B). Die Punkte M1, M2, A,B werden miteinander verbunden.
a) Analysieren Sie die geometrischen Eigenschaften der entstandenen Figur.
b) Beschreiben Sie, in welcher Weise diese Figur bei der Behandlung geometrischer Grundkonstruktionen Anwendung finden kann.
2. Erläutern Sie die didaktische Funktion des Konstruierens in der Hauptschule anhand typischer Konstruktionsaufgaben.
3. Entwickeln Sie eine Unterrichtseinheit für die 8. Jahrgangsstufe, in der die Konstruktion eines Dreiecks aus drei gegebenen Seiten behandelt wird.
4. Gegeben sind zwei sich schneidende Gerade g1 und g2, wobei der Schnittpunkt S außerhalb des Zeichenblattes liegen soll.
a) Beschreiben Sie ein Verfahren zur Konstruktion einer Winkelhalbierenden von g1 und g2. Begründen Sie dieses Verfahren.
b) Charakterisieren Sie das Winkelhalbierendenpaar zweier Geraden als geometrischen Ort aller Punkte mit einer kennzeichnenden Eigenschaft (Begründung),
1989/II,2
1. a) Erklären Sie den Begriff rationaler Zahl. Geben Sie verschiedene Darstellungsweisen für rationale Zahlen an.
b) Was heißt es, den Bruch
- als Maßzahl von Größen
- als Angabe über ein Größenverhältnis
- als Operator in einem Größenbereich
aufzufassen?
2. Entwickeln Sie eine Lernsequenz zum Aufbau des Bruchzahlbegriffs.
3. Skizzieren Sie eine Übungsstunde zum Thema Addieren und Subtrahieren von Bruchzahlen.
4. a) Erklären Sie die Begriffe: natürliche Zahl, ganze Zahl, irrationale Zahl und reelle Zahl.
b) Gegeben sei ein Rechteck mit ganzzahligen Seitenlängen a und b. Untersuchen Sie, zu welchen Zahlenbereichen die Längen der Diagonalen dieses Rechtecks gehören.
1989/II,3
1. a) Erläutern Sie den Begriff Prisma.
b) Beschreiben Sie wichtige Lernziele für die Behandlung von Prismen im Unterricht.
2. Diskutieren Sie Möglichkeiten für die unterrichtliche Erarbeitung der Volumenformel des geraden Prismas.
3. Entwerfen Sie eine Unterrichtseinheit mit dem Ziel, anhand verschiedener Dachformen bei Häusern Kenntnisse über Prismen und Pyramiden zu vertiefen.
4. Konstruieren Sie Schrägbild und Dreitafeldarstellung eines Walmdachs (vgl. Skizze), bei dem die beiden längsten Kanten zu 10 LE und die übrigen 7 Kanten zu je 5 LE gemessen wurden.
>> Zum Anfang
1989/I,1
1. a) Erklären Sie den Begriff "Symmetrie Figur" im Bereich der ebenen Geometrie! Unterscheiden Sie dabei verschiedene Symmetriearten!
b) Diskutieren Sie die Bedeutung des Symmetriebegriffs im Mathematikunterricht!
2. Entwerfen Sie eine Unterrichtseinheit, in der die Eigenschaften achsensymmetrischer Figuren erarbeitet werden!
3. Beschreiben Sie Lernzielkontrollen zum Thema "Symmetrische Figuren"!
4. a) Klassifizieren Sie die Vierecke mit Hilfe von Symmetrieeigenschaften!
b) Geben Sie für folgende Figurentypen jeweils alle ebenen Kongruenzabbildungen an, die diese Figuren auf sich selbst abbilden (Deckabbidungen): gleichseitiges Dreieck, Parallelogramm, Raute, Trapez, Kreis.
c) Zeigen Sie, daß die Deckabbildungen der Raute eine Gruppe bilden!
1989/I,2
1. a) Definieren Sie die Begriffe Kreislinie, Kreisfläche, Kreisumfang und Kreisinhalt!
b) Beschreiben Sie unterrichtliche Verfahren zur näherungsweisen Bestimmung des Kreisumfangs!
2. Die Kreiszahl p kann sowohl im Zusammenhang mit der Berechnung des Kreisumfangs als auch des Kreisinhalts eingeführt werden. Beschreiben Sie beide Verfahren!
3. Beschreiben Sie die unterrichtliche Behandlung folgende Sachaufgabe: der Stundenzeiger einer Turmuhr ist 3,5 m lang, der Minutenzeiger 4 m. Welchen Weg legen die Zeigerspitzen in jeweils 2 Stunden 20 Minuten zurück?
4. a) Gegeben sei ein Kreissektor mit Radius r und Bodenlänge b. Leiten Sie eine Formel zur Berechnung des Sektorinhalts her!
b) Stellen Sie eine Beziehung zu dem Flächeninhalt des Dreiecks her!
c) Entwickeln Sie eine Formel für den Inhalt der Mantelfläche eines geraden Kreiskegels mit Grundkreisradius ? und Höhe h.
1989/I,3
1. a) Geben Sie verschiedene Sachsituationen an, in denen man sich für Anteile interessiert! Wie läßt sich der Begriff "Anteil" mathematisch präzisieren?
b) Nennen Sie Beispiele aus dem Sachrechnen, bei denen Anteile addiert werden sollen!
c) Wie bestimmt man "Anteile von Anteilen"? Geben Sie Beispiele!
2. Nennen Sie verschiedene Themenbereiche des Mathematikunterrichts der Hauptschule, in denen der Anteilbegriff eine Rolle spielt, und geben Sie dazu Erläuterungen!
3. Ein Landwirt bewirtschaftet eine Fläche von 30 ha. 60% der Fläche sind für Getreideanbau vorgesehen.
dieser Fläche werden mit Weizen angebaut."
a) Nennen Sie zu dieser Sachsituation mögliche Aufgabenstellungen, in denen der Anteilbegriff zum Tragen kommt!
b) Skizzieren Sie eine Unterrichtseinheit, in der diese Aufgabenstellungen behandelt werden!
4. Aus zwei Mengen Gold mit Gewicht m1 und Feingehalt k1 bzw. mit Gewicht m2 und Feingehalt k2 soll eine Legierung zusammengeschmolzen werden.
a) Bestimmen Sie den Feingehalt k der entstehenden Legierung!
b) Geben Sie das Mischungsverhältnis
in Abhängigkeit von den Feingehalten an!
c) Wo treten bei diesen Aufgaben Anteile auf?
>> Zum Anfang
1988/II,1
1. a) Geben Sie eine Definition für den Begriff des regelmäßigen Vielecks!
b) Konstruieren Sie ein regelmäßiges Achteck, und begründen Sie die Konstruktionsschritte!
2. Erläutern Sie verschiedene thematische Zusammenhänge, in denen das regelmäßige Sechseck im Mathematikunterricht der Hauptschule behandelt werden kann!
3. a) Beschreiben Sie unterschiedliche Wege, wie Hauptschüler die Größe des Innenwinkels bei einem regelmäßigen Sechseck bestimmen können!
b) Gehen Sie bei diesen Wegen auf die unterschiedlichen Anforderungen, Voraussetzungen und Chancen für das selbständige Lösen dieses Problems ein!
c) Wie kann man den Schülern einsichtig machen, daß die Ebene mit kongruenten regelmäßigen Sechsecken parkettiert werden kann?
4. a) Geben Sie die Symmetrien eines regelmäßigen Sechsecks an!
b) Begründen Sie, daß man den Radius eines Kreises genau sechsmal auf dem Kreis abtragen kann!
1988/II,2
1. Erläutern und begründen Sie das Normalverfahren
a) für die schriftliche Addition von Dezimalbrüchen,
b) für die schriftliche Division von Dezimalbrüchen!
2. Beschreiben Sie unterrichtsmethodische Zugänge zur Multiplikation von Dezimalbrüchen!
3. Entwickeln Sie eine Unterrichtseinheit zur Einführung in das Dividieren durch Dezimalbrüche!
4. Beschreiben und begründen Sie, wie man gewöhnliche Brüche in Dezimalbrüche und umgekehrt umwandeln kann!
1988/II,3
1. Erläutern Sie die Begriffe
a) direkte Proportionalität
b) indirekte Proportionalität
2. Beschreiben Sie anhand geeigneter Beispiele verschiedene Methoden für das Lösen von Sachaufgaben zur direkten und indirekten Proportionalität!
3. Skizzieren Sie eine Unterrichtseinheit, in der die Fähigkeit zur Unterscheidung von direkter Proportionalität zu anderen Wachstumsfunktionen gefördert wird.
4, Die Gleichung z = k × x × y (k ist eine Konstante) beschreibt funktionale Abhängigkeiten zwischen den Größen x,a und z. Zeigen Sie, daß durch Spezialisierung der Gleichung direkte und indirekte Proportionalitäten sowie quadratische Abhängigkeiten dargestellt werden können, und erläutern Sie dies an Beispielen!
>> Zum Anfang
1988/I,1
1. a) Geben Sie verschiedene Herleitungen der Regel für die Division eines gewöhnlichen Bruches durch einen gewöhnlichen Bruch! Beschreiben Sie die zugrundeliegenden Bruchauffassungen!
b) Diskutieren Sie diese Verfahren im Hinblick auf den Mathematikunterricht der Hauptschule!
c) Nennen und diskutieren Sie unterschiedliche Formulierungsmöglichkeiten für die Bruchrechenregeln!
2. Erläutern Sie Schwierigkeiten bei der Behandlung des Themas "Division von Brüchen" in der Hauptschule!
3. Erläutern Sie die folgenden Schülerfehler:
a)
Worin sehen Sie die Ursachen für diese Fehler? Welche Maßnahmen schlagen Sie zu ihrer Überwindung vor?
4. Begründen Sie mit Hilfe der Bruchrechenregeln die Formeln
a)
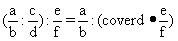
b)
1988/I,2
1. G1 und G2 seien Größenbereiche.
a) Beschreiben Sie direkte und indirekte Proportionalitäten als Abbildungen von G1 nach G2 durch die Angabe von Funktionsgleichungen!
b) Erläutern und begründen Sie die Dreisatzmethode an je einem selbstgewählten Beispiel!
2. Die Grundaufgaben der Prozentrechnung lassen verschiedene Lösungsverfahren zu: Dreisatzmethode, Operatormethode und Fomelansatz. Diskutieren Sie Vor- und Nachteile dieser Verfahren im Hinblick auf ihren unterrichtlichen Einsatz!
3. Skizzieren Sie eine Unterrichtseinheit zur Behandlung folgender Sachaufgabe: Der Aushub einer großen Baugrube kann von 10 Lastkraftwagen bei einer täglichen Einsatzzeit von 8 Stunden in 14 Tagen abtransportiert werden.
a) Um wieviele Tage verlängert sich der Abtransport, wenn nur 8 Fahrzeuge an der Baustelle eingesetzt werden und wenn diese nur 7 Stunden pro Tag fahren können?
b) Wieviele Stunden müßten diese 8 Lastkraftwagen täglich fahren, wenn die Arbeit in den ursprünglich vorgesehenen 14 Arbeitstagen beendet sein soll?
4. Nennen Sie für direkte und indirekte Proportionalitäten kennzeichnende Bedingungen! Leiten Sie diese Bedingungen aus den entsprechenden Funktionsgleichungen ab!
1988/I,3
1. a) Leiten Sie mit Hilfe der Formel für den Rauminhalt eines Quaders die Formel für den Rauminhalt gerader Prismen her!
b) Beschreiben Sie, wie man die Gültigkeit der Formel aus 1a) auch für schiefe Prismen nachweist!
2. a) Beschreiben Sie Aktivitäten zur Einführung des Begriffs Rauminhalt!
b) Zeigen Sie, wie man im Unterricht schrittweise die Formel für den Rauminhalt eines Quaders herleiten kann!
3. Entwickeln Sie eine Unterrichtseinheit für die Erarbeitung der Formel für den Rauminhalt eines geraden Prismas mit dreieckiger Grundfläche!
4. Skizzieren Sie, wie man am Quader in das Arbeiten mit Schrägbildern (u.a. Konstruktionsvorschriften) einführen kann!
1987/II,1
1. a) Geben Sie Beispiele von Formeln aus verschiedenen Bereichen der Hauptschulmathematik!
b) Diskutieren Sie die unterrichtliche Bedeutung von Formeln!
2. Entwickeln Sie eine Unterrichtseinheit zur Erarbeitung der Prozentformel
(p Prozentwert, G Grundwert, p Prozentsatz)!
3. Beschreiben Sie Möglichkeiten für die operative Durcharbeitung der Prozentformel!
4. a) Diskutieren Sie rechnerische und graphische Aspekte der Funktion y = ax + b!
b) Geben Sie konkrete Situationen an, die sich mit dieser Funktion beschreiben lassen! Interpretieren Sie dabei jeweils auch die Variablen y,x und die Koeffizienten a,b!
1987/II,2
1. a) Geben Sie verschiedenartige Definitionen des rechten Winkels!
b) Diskutieren Sie ihre Verwendung im Unterricht der Hauptschule!
2. Beschreiben Sie Begriffe aus dem Geometrieunterricht der Hauptschule, bei denen der rechte Winkel eine Rolle spielt!
3. Arbeiten Sie eine Unterrichtseinheit zur Einführung des rechten Winkels in der 5. Jahrgangsstufe aus!
4. Zeigen Sie: Ein Innenwinkel im Dreieck ist genau dann ein rechter Winkel, wenn die dem Scheitel des Winkels gegenüberliegende Seite zweimal so lang ist, wie die durch den Scheitel gehende Seitenhalbierende!
1987/II,3
1. Erläutern Sie anhand von Beispielen den Begriff: "Größenbereich mit Teilbarkeitseigenschaft"!
2. Beschreiben Sie die methodische Verwendung von Größen
a) beim Aufbau des Bruchzahlbegriffs,
b) bei der Einführung der Kleinerrelation zwischen Bruchzahlen!
3. Entwerfen Sie eine Unterrichtssequenz zur Einführung der Addition von Bruchzahlen!
4. a) Geben Sie Beziehungen an zwischen den Mengen der ganzen Zahlen, der rationalen Zahlen, der Bruchzahlen, der natürlichen Zahlen, der reellen Zahlen und der irrationalen Zahlen!
b) Zu welchen dieser Mengen gehören die Zahlen
>> Zum Anfang
1987/I,1
1. Zur ebenen Darstellung von Körpern kann man Schrägbilder und Mehr-Tafelprojektionen benützen.
a) Erläutern Sie beide Darstellungsformen am Beispiel des Quaders.
b) Diskutieren Sie ihre Vor- und Nachteile!
2. Skizzieren Sie eine Unterrichtseinheit zum Thema Schrägbild des Tetraeders!
3. a) Diskutieren Sie die Entwicklung von Raumwahrnehmung und Raumvorstellung als Ziele des Geometrieunterrichts!
b) Beschreiben Sie formkundliche Aktivitäten am Würfel, die der Schulung der Raumvorstellung dienen!
4. Gegeben sei ein Quader (a = 6 cm, b = 4 cm, c = 3 cm). Beschreiben Sie ein konstruktives und ein rechnerisches Verfahren zur Bestimmung der Länge der Raumdiagonalen!
1987/I,2
1. Beschreiben und erklären Sie die Darstellung natürlicher Zahlen im Stellenwertsystem!
2. a) Formulieren Sie Ziele für die Behandlung der Stellenwertschreibweise natürlicher Zahlen in der 5. Jahrgangsstufe!
b) Geben Sie geeignete Aufgabenstellungen an, die der Realisierung dieser Ziele dienen!
3. a) Beschreiben und begründen Sie an einem Beispiel das Normalverfahren der schriftlichen Division!
b) Erläutern Sie an Beispielen Schwierigkeiten, die bei diesem Verfahren auftreten können. Geben Sie Maßnahmen zu ihrer Behebung an!
4. Geben Sie eine Übersicht über Gesetze und Regeln für das Rechnen mit natürliche Zahlen! Zeigen Sie exemplarisch, wo diese Gesetze und Regeln im Mathematikunterricht der Hauptschule Anwendung finden!
1987/I,3
1. a) Nennen Sie verschiedene Typen von Bewegungsaufgaben für einen und für zwei bewegte Körper, die in der Hauptschule vorkommen. Geben Sie für jeden Typ eine Beispielaufgabe an.
b) Welche Funktionstypen liegen in den einzelnen Fällen vor? Welche physikalischen Annahmen über die Art der Bewegung werden bei diesen Bewegungsaufgaben gemacht?
2. Diskutieren Sie die inhaltlichen und formalen Kenntnisse und Fähigkeiten, die zur Lösung von Bewegungsaufgaben erforderlich sind. Gehen Sie auf besondere Schwierigkeiten ein.
3. a) Erläutern Sie für die Aufgabentypen mit zwei bewegten Körpern jeweils eine Lösungsmethode.
b) Welche Gründe sprechen dafür, daß jede arithmetische Lösung einer Bewegungsaufgabe von einer graphischen Lösung im Weg-Zeit-Diagramm begleitet sein sollte?
c) Welche Eigenschaften einer Bewegung kann man aus einem Weg-Zeit-Diagramm ablesen? Diskutieren Sie verschiedene Bewegungsarten.
>> Zum Anfang
1986/II,1
1. a) Erläutern Sie den Begriff der Abbildung einer Ebene auf sich!
b) Beschreiben Sie die verschiedenen ebenen Kongruenzabbildungen!
2. a) Geben Sie die wichtigsten Eigenschaften der Achsenspiegelung an!
b) Erläutern Sie, wie man Eigenschaften der Achsenspiegelung in der Hauptschule erarbeiten kann!
3. Entwickeln Sie eine Unterrichtseinheit für die Erarbeitung der Eigenschaften eines gleichschenkligen Trapezes mit Hilfe der Achsenspiegelung!
4. Wie können die ebenen Kongruenzabbildungen mit Hilfe von Achsenspiegelungen erzeugt werden?
1986/II,2
1. a) Erläutern Sie die Begriffe Kreiszylinder und gerader Kreiszylinder!
b) Welche Symmetrien hat ein gerader Kreiszylinder?
c) Welche Form kann die Schnittfläche einer Ebene mit einem geraden Kreiszylinder haben (Fallunterscheidung)?
2. a) Beschreiben und begründen Sie einen hauptschulgerechten Weg zur Berechnung des Volumens eines geraden Kreiszylinders!
b) Wie kann man im Unterricht zeigen, daß für schiefe und gerade Kreiszylinder die gleiche Volumenformel gilt?
3. Erläutern Sie, welche Probleme sich beim Zeichnen des Schrägbildes eines geraden Zylinders für die Schüler ergeben (Fallunterscheidung)!
4. a) Leiten Sie eine Formel für das Volumen des Kegelstumpfes her!
b) Zeigen Sie, wie sich daraus als Grenzfall die Volumenformel des geraden Kreiszylinders ergibt!
1986/II,3
1. a) Erläutern Sie die dezimale Darstellung der Bruchzahlen (Fallunterscheidung)!
b) Wie lassen sich gewöhnliche Brüche in Dezimalbrüche umwandeln?
c) Wie kann man umgekehrt abbrechende Dezimalbrüche in gewöhnliche Brüche umwandeln?
>> Zum Anfang
1986/I,1
1. Erklären Sie die Begriffe Aussage, Aussageform und Term! Zeigen Sie ihre Bedeutung für die Behandlung von Gleichungen und Ungleichungen!
2. Beschreiben Sie Methoden für das Lösen von Gleichungen, die für den Unterricht in der Hauptschule relevant sind!
3. Erläutern und diskutieren Sie die Funktion des sogenannten Waage-Modells bei der Behandlung von Äquivalenzumformungen von Gleichungen!
4. Skizzieren Sie eine Unterrichtseinheit für die 8. Jahrgangsstufe, in der Gleichung
gelöst wird!
1986/I,2
1. a) Nennen Sie Diagonaleneigenschaften, die im Zusammenhang mit speziellen Viereckstypen eine Rolle spielen!
b) Definieren Sie das Drachenviereck, die Raute, das Rechteck und das Quadrat jeweils ausschließlich mit Hilfe von Diagonaleneigenschaften!
c) Ein Viereck, dessen Diagonalen einander halbieren, heißt "Parallelogramm". Zeigen Sie, daß diese Definition mit einer der in der Hauptschule üblichen Definitionen äquivalent sind!
2. Beschreiben Sie Schüleraktivitäten, die zum Aufbau des Begriffs "Trapez" führen!
3. Skizzieren Sie eine Unterrichtseinheit zur Flächeninhaltsberechnung des Trapezes! dabei soll u.a. auf folgende Punkte eingegangen werden: Unterrichtsvoraussetzungen, Lernzielsequenz, Arbeitsmittel, Lernzielkontrollen, einschlägige Anwendungen.
4. a) Beweisen Sie: Die Mittelparallele eines Trapezes halbiert die beiden Diagonalen.
b) Beweisen Sie: Das achsensymmetrische Trapez besitzt einen Umkreis. Geben Sie eine Vorschrift zur Konstruktion des Umkreises!
1986/I,3
1. Zwei Zahlenpaare (a,b) und (c,d) mit a,b,c,d e N heißen äquivalent, wenn a × d = b × c ist!
a) Zeigen Sie, daß dadurch eine Äquivalenzrelation definiert ist!
b) Erklären Sie in diesem Zusammenhang das Erweitern und Kürzen von Brüchen!
2. Welche Bedeutung kommt dem Erweitern und Kürzen von Brüchen zu?
3. Entwickeln Sie eine Unterrichtssequenz zum Thema Kürzen und Erweitern in der 6. Jahrgangsstufe!
4. a) Wie kann man mit Hilfe der Primfaktorenzerlegung das kgV (kleinstes gemeinsames Vielfache) und den ggT (größter gemeinsamer Teiler) zweier Zahlen a und b aus N finden?
b) Zeigen Sie: kgV(a,b) × ggT(a,b) = a × b.
>> Zum Anfang
1985/II,1
1. Wie kann man den Begriff "Flächeninhalt ebener Vielecke" mathematisch entwickeln?
2. Skizzieren Sie eine Unterrichtseinheit zum Thema "Berechnung der Rechtecksfläche"!
3. Zeigen Sie am Beispiel der Formel für die Rechtecksfläche unterrichtliche Möglichkeiten für die Betrachtung funktionaler Abhängigkeiten auf!
4. Rechtecksflächen werden im Mathematikunterricht zur Veranschaulichung nicht-geometrischer Sachverhalte herangezogen. Erläutern Sie dies an geeigneten Beispielen!
5. a) Zeigen Sie, daß das Quadrat unter allen umfangsgleichen Rechtecken den größten Flächeninhalt besitzt!
b) Wie kann man Schüler diese Extremaleigenschaft des Quadrats entdecken lassen=
1985/II,2
1. In der Wirtschaft werden Warenmengen Preise zugeordnet. Erläutern Sie an einigen charakteristischen Beispielen verschiedene Funktionsarten, die dabei auftreten können (jeweils auch mit graphischer Darstellung)!
2. a) Formulieren Sie Lernziele für die Behandlung von Ware-Preis-Funktionen in der Hauptschule!
b) Geben Sie Lernzielkontrollen in Form von Aufgaben an!
3. Entwickeln Sie eine Unterrichtseinheit zum Thema "Briefporto" auf der Grundlage folgende Tabelle
Postgebühren, Stand: 1. September 1983
DM
Briefe Standardbriefe*) 0,80
andere Briefe bis 50 g 1,30
über 50 bis 100 g 1,90
über 100 bis 250 g 2,50
über 250 bis 500 g 3,10
über 500 bis 1000 g 3,70
*)Briefsendungen bis 20g: Länge zwischen 14 und 23,5 cm, Breite zwischen 9 und 12 cm, Höhe bis 0,5 cm; Länge mindestens das 1,4fache der Breite.
4. a) Erläutern Sie wichtige Darstellungsformen von Funktionen!
b) Diskutieren Sie, welche Eigenschaften von Funktionen in den Darstellungsformen besonders gut zum Ausdruck kommen!
1885/II,3
1. Erläutern Sie einen mathematischen Zugang zur Formel des Kreisumfanges!
2. Entwickeln Sie eine Unterrichtseinheit für eine hauptschulgemäße Einführung der Kreisumfangsformel!
3. Entwerfen Sie Aufgaben, die der Übung, Anwendung und Vertiefung der Kreisumfangsformel dienen!
4. a) Skizzieren Sie eine unterrichtliche Herleitung der Kreisflächenformel, die von der Kenntnis der Kreisumfangsformel ausgeht!
b) Erläutern Sie das Problem der "Quadratur des Kreises"!
>> Zum Anfang
1985/I,1
1. a) Erklären Sie den allgemeinen Begriff Kegel.
b) Welche Schüleraktivitäten sind für den Aufbau des Begriffs Kreiskegel förderlich?
2. a) Skizzieren Sie ein mathematisches Verfahren zur Volumenbestimmung eines geraden Kreiskegels.
b) Erläutern Sie, wie man die in der Volumenformel für den Kreiskegel beschriebenen funktionalen Abhängigkeiten im Unterricht erarbeiten kann.
3. Skizzieren Sie eine Unterrichtseinheit zur Entwicklung der Oberflächenformel eines geraden Kreiskegels.
4. Ein kegelförmiger Meßbecher von 1 l Fassungsvermögen hat eine Höhe von 20 cm. An einer Mantellinie sollen Markierungen für
angebracht werden. Welche Abstände haben die Markierungen von der Spitze des Meßbechers?
1985/I,2
1. Formulieren und begründen Sie die Regeln für die Teilbarkeit durch 3, 4 und 18.
2. Entwickeln Sie eine Unterrichtssequenz zur "Neunerregel", bei der folgende Punkte genauer darzulegen sind: Sachliche Voraussetzungen, Lernziele, Einstieg, Veranschaulichung, Arbeits- und Übungsformen.
3. Wie kann ein Schüler zur Einsicht in folgenden Sachverhalt geführt werden: Ist eine Zahl durch 3 und durch 4 teilbar, so ist sie auch durch 12 teilbar; ist eine Zahl durch 6 und durch 4 teilbar, so ist sie nicht in jedem Fall durch 24 teilbar.
4. Geben Sie je eine zur Teilbarkeit durch 9 bzw. 10 im Dezimalsystem analoge Regel im g-adischen Stellenwertsystem an. Beweisen Sie diese Regeln.
1985/I,3
1. a) Erklären Sie den Begriff Größenbereich und erläutern Sie ihn an Beispielen.
b) Was versteht man unter Teilbarkeitseigenschaft bzw. Kommensurabilität? Welche der beiden Eigenschaften besitzen die Größenbereiche der Längen bzw. der Geldwerte?
2. a) Im Unterricht sind Proportionalitäten und Antiproportionalitäten wichtige Abbildungen von Größenbereichen. Charakterisieren Sie beide Abbildungen.
b) Diskutieren Sie ihr Vorkommen im Erfahrungsbereich der Schüler.
c) Vergleichen Sie verschiedene Darstellungsmöglichkeiten dieser Abbildungen hinsichtlich ihrer didaktischen Funktion.
3. Entwickeln Sie eine Folge von Aufgaben, die der operativen Durcharbeitung der Proportionalitäten dient und erklären Sie daran das sogenannte operative Prinzip.
4. a) Erklären Sie den Zusammenhang zwischen Proportionalität, Bruchoperator und Prozent.
b) Wie lauten die drei Grundaufgaben der Prozentrechnung? Zu ihrer Lösung werden die Dreisatzmethode und die Operatormethode benutzt. Stellen Sie beide Verfahren dar und diskutieren Sie ihre Vor- und Nachteile.
>> Zum Anfang
1984/II,1
1. a) Welche Fälle der dezimalen Darstellung einer Bruchzahl können auftreten? Geben Sie Beispiele dazu an!
b) Geben Sie Verfahren an, wie gewöhnliche Brüche in Dezimalbrüche verwandelt werden können.
c) Wie lassen sich abbrechende Dezimalbrüche in gewöhnliche Brüche umwandeln?
2. a) Geben Sie Probleme aus dem Mathematikunterricht der Hauptschule an, die auf unendliche, nicht periodische Dezimalbrüche führen!
b) Beschreiben Sie für eines dieser Probleme die Behandlung im Unterricht (Näherungsverfahren)!
3. Skizzieren Sie eine Lernsequenz zur Erarbeitung der Regel für die Multiplikation von Dezimalbrüchen!
4. Zeigen Sie an Beispielen auf, wie die Regeln für die Grundrechenarten mit abbrechenden Dezimalbrüchen über das Rechnen mit gewöhnlichen Brüchen im Unterricht der Hauptschule gewonnen werden können!
1984/II,2
1. a) Nennen Sie wichtige Eigenschaften des Parallelogramms!
b) Geben Sie verschiedene Möglichkeiten an, das Parallelogramm zu definieren!
2. Erläutern Sie Beziehungen zwischen dem Parallelogramm und den anderen Vierecken! Stellen Sie diese Beziehungen in einem Diagramm dar!
3. Beschreiben Sie eine unterrichtliche Möglichkeit für den Aufbau des Begriffs "Parallelogramm" im Mathematikunterricht der Hauptschule (Lehreraktivitäten, Schüleraktivitäten)!
4. "Die vier Winkelhalbierenden eines Parallelogramms ABCD, das keine Raute ist, schließen ein Rechteck PQRS ein." Beweisen Sie diesen Satz unter Angabe der benutzten Voraussetzungen! Weshalb wurde in der Formulierung des Satzes die Raute ausgeschlossen?
1984/II,3
1. a) Definieren Sie das arithmetische Mittel aus n Größen x1,...,xn!
b) Kann man das arithmetische Mittel aus drei Größen x1, x2, x3 berechnen, indem man zunächst das Mittel A aus x1 und x2 bildet und dann A und x3 mittelt?
c) Zeigen Sie, daß das arithmetische Mittel zweier Zahlen a und b von diesen Zahlen gleichen Abstand hat!
2. a) Wie kann man im Unterricht zeigen, daß im Trapez die Länge der Mittellinie gleich dem arithmetischen Mittel der Längen der beiden Grundlinien ist?
b) Nennen Sie typische Anwendungen des arithmetischen Mittels im Sachrechnen!
3. Skizzieren Sie für das 9. Schuljahr eine Einführung des arithmetischen Mittels bei der Auswertung einer statistischen Erhebung!
4. a) Sei a < b < c und m das arithmetische Mittel dieser drei Zahlen. Bestimmen Sie (m-a) + (m- b) + (m - c), und erläutern Sie das Ergebnis!
b) Zeigen Sie, wie man mit Hilfe des arithmetischen Mittels ein Verfahren zur näherungsweisen Bestimmung von Quadratwurzeln entwickeln kann!
>> Zum Anfang
1984/I,1
1. a) Erklären Sie den Begriff Pyramide!
b) Geben Sie eine Übersicht über die wichtigsten sachlichen Aspekte (Begriffe, Größen, Darstellungsmittel), die bei der Behandlung der Pyramide im Unterricht eine Rolle spielen!
2. Beschreiben Sie verschiedenartige Schüleraktivitäten, die für den Aufbau des Begriff Pyramide förderlich sind! Geben Sie auch deren didaktische Bedeutung an!
3. Skizzieren Sie eine Unterrichtssequenz zur Entwicklung und Begründung der Formel für das Volumen einer Pyramide! Diskutieren Sie auftretende Probleme!
4. Skizzieren Sie eine mathematisches Verfahren zur Bestimmung des Volumens einer Pyramide!
1984/I,2
1. Erklären Sie den Begriff "Gleichung mit einer Variablen"!
2. a) Skizzieren Sie Lösungsverfahren für lineare Gleichungen mit einer Variablen, die
- in einer propädeutischen
- in einer systematischen
Gleichungslehre im Unterricht der Hauptschule Anwendung finden!
b) Diskutieren Sie die Rolle der Probe im Hinblick auf diese Lösungsverfahren!
3. Begründen Sie auf schülergemäßem Niveau: "Die Lösungsmenge einer Gleichung ändert sich nicht, wenn man auf beiden Seiten der Gleichung dieselbe Zahl oder dieselbe Variable addiert".
4. Folgende Sachaufgabe soll mit Hilfe eines Gleichungsansatzes gelöst werden: Der Umfang eines Rechtecks beträgt 188 m. Die eine Seite des Rechtecks ist dreimal so lang wie die andere. Wie lang sind die Seiten des Rechtecks? Entwickeln Sie hierzu eine Unterrichtseinheit!
5. Welche Probleme treten beim Lösen linearer Gleichungen und linearer Ungleichungen, jeweils mit einer Variablen, im Bereich der ganzen Zahlen auf?
1984/I,3
1. Erläutern Sie folgende Begriffe:
a) Variable (Platzhalter)
b) Term und Termwert
c) Termumformung und Termwertberechnung.
2. Welche Bedeutung haben die Begriffe Variable und Term im Rahmen der Hauptschulmathematik?
3. Arbeiten Sie eine Unterrichtseinheit aus, die das Verständnis von Buchstabenvariablen zum Ziel hat!
4. Bei der Berechnung des Flächeninhalts eines Trapezs kann man zu folgenden Termen gelangen:
Erläutern Sie auch anhand von Zeichnungen die zugehörigen geometrischen Überlegungen!
>> Zum Anfang
1983/II,1
1. a) Stellen Sie mit Hilfe von Operatoren die Grundaufgaben der Prozentrechnung dar und zeigen Sie, wie man diese löst.
b) Beschreiben Sie, wie man Taschenrechner bei der Lösung der Grundaufgaben vorteilhaft benutzen kann.
2. Nennen Sie wichtige Anwendungsbereiche der Prozentrechnung und erläutern Sie deren Bedeutung für die Schüler. Geben Sie jeweils eine typische Aufgabe an.
3. Den Grundaufgaben der Prozentrechnung liegen direkt oder indirekt proportionale Zuordnungen zugrunde.
a) Erläutern Sie dies an geeigneten Zahlenbeispielen.
b) Zeigen Sie daran Möglichkeiten für die Untersuchung funktionaler Abhängigkeiten im Mathematikunterricht auf.
4. a) Zeigen Sie, wie man die Zinsformel
(K: Kapital, p: Zinssatz, Z: Zinsen) im Unterricht herleiten kann.
b) Geben Sie eine Formel zur Berechnung der Zinsen für n Tage an. Welche Annahmen liegen ihr zugrunde? Wie kann man diese Formel mit den Schülern erarbeiten?
1983/II,2
1. a) Geben Sie drei inhaltlich verschiedene Beispiele aus der Erfahrungswelt der Schüler an, bei denen Winkel auftreten und erläutern Sie diese Beispiele.
b) Entwickeln Sie anhand dieser Beispiele zwei Winkeldefinitionen.
2. a) Beweisen Sie auf zwei verschiedenen Weisen den Satz: Die Summe der Innenwinkel im Dreieck beträgt 180°.
b) Leiten Sie je eine Formel für die Summe der Innen- und die Summe der Außenwinkel eines n-Ecks ab.
3. a) Begründen Sie fachlich die Grundkonstruktion zur Halbierung eines Winkels.
b) Beschreiben Sie die Winkelhalbierende als geometrischen Ort (mit Beweis).
4. Entwickeln und begründen Sie eine Unterrichtssequenz zur Einführung in die Winkelsumme im Dreieck.
1983/II,3
1. a) Definieren Sie mit Hilfe der Achsenspiegelung die Kongruenz zweier ebener Figuren.
b) Zeigen Sie, daß die Relation "... ist konsequent zu ..." in der Menge aller Dreiecke eine Äquivalenzrelation ist.
2. a) Wie lauten die Kongruenzsätze für Dreiecke?
b) Erläutern Sie folgende Aussage: "Ein Dreieck ist aus der Länge der drei Seiten eindeutig konstruierbar".
3. Beweisen Sie (mit Hilfe der Achsenspiegelung) einen Kongruenzsatz für Dreiecke.
4. Skizzieren Sie eine Unterrichtseinheit, in der die Konstruktion eines Dreiecks aus den drei Seitenlängen eingeführt wird. Folgende Punkte sind genauer zu behandeln:
a) Das Problem der Motivation durch die Auswahl eines geeigneten Beispiels.
b) Knappe Darstellung des geplanten Unterrichtsablaufs einschließlich einer Lernzielsequenz.
c) Die Erarbeitung einer schülergemäßen Konstruktionsbeschreibung.
>> Zum Anfang
1983/I,1
Bruchzahlen können im Unterricht der Hauptschule über konkrete Brüche ("Größenkonzept") oder Bruchoperatoren "Operatorkonzept") eingeführt werden.
1. Erläutern Sie die Begriffe konkreter Bruch, Bruchoperator und Bruchzahl.
2. Geben Sie Lernschritte für die unterrichtliche Erarbeitung des Bruchoperators an.
3. Diskutieren Sie die beiden in der Einleitung genannten Konzepte hinsichtlich ihrer Eignung für die Einführung in die Multiplikation von Bruchzahlen.
4. Skizzieren Sie eine Unterrichtseinheit zur Einführung in die Multiplikation von Bruchzahlen.
5. a) Erläutern Sie die Auffassung der Bruchzahlen als Klassen von Zahlenpaaren.
b) Welche Bedeutung hat diese Auffassung im Unterricht der Hauptschule?
1983/I,2
1. a) Was versteht man unter einem allgemeinen Zylinder und was speziell unter einem geraden Kreiszylinder als geometrische Körper?
b) Welche Formen kann die Schnittfläche einer Ebene mit einem geraden Kreiszylinder haben? (Fallunterscheidung)
c) Welche Symmetrieeigenschaften hat ein gerader Kreiszylinder?
d) Wie kann man zeigen, daß für schiefe und gerade Zylinder die gleiche Volumenformel gilt?
2. Beschreiben und begründen Sie einen hauptschulgerechten Weg zur Berechnung der Oberfläche des Zylinders und kennzeichnen Sie dabei besonders diejenigen Lernschritte, die dem Schüler möglicherweise Schwierigkeiten bereiten.
3. Wie kann man im Unterricht Schüler entdecken lassen, daß es unter den Zylindern mit gleichem Volumen einen mit kleinster Oberfläche gibt?
1983/I,3
1. Nennen Sie wichtige Teilbarkeitsregeln, die sich auf die Darstellung der natürlichen Zahlen im Zehnersystem beziehen, und klassifizieren Sie diese.
2. Begründen Sie die Teilbarkeitsregeln für 8,9 und 10.
3. Erläutern Sie die Bedeutung dieser Teilbarkeitsregeln: Lernziele, Anwendungsbereiche, Kontrollfunktion.
4. Erstellen Sie einen Unterrichtsentwurf für die Behandlung der Teilbarkeit durch 15.
5. Formulieren und begründen Sie Teilbarkeitsregeln bei der Darstellung der natürlichen Zahlen im Zehnersystem mit der Basis 6.
>> Zum Anfang
1982/II,1
1. a) Erläutern Sie den Begriff der Abbildung einer Ebene auf sich.
b) Geben Sie eine Übersicht über die ebenen Kongruenzabbildungen.
2. Geben Sie die wichtigsten Eigenschaften der Achsenspiegelung an.
3. Wie können die ebenen Kongruenzabbildungen mit Hilfe von Achsenspiegelungen erzeugt werden?
4. Erläutern Sie, mit welchen Methoden man Eigenschaften der Achsenspiegelung in der Hauptschule erarbeiten kann.
5. Entwickeln Sie ein Unterrichtsbeispiel für die Erarbeitung der Eigenschaften eines Drachens mit Hilfe der Achsenspiegelung.
1982/II,2
Im Sachrechnen der Hauptschule beschäftigt sich ein Aufgabengebiet mit den Beziehungen zwischen den Größen Weg, Zeit und Geschwindigkeit.
1. a) Geben Sie einige typische Beispiele für Bewegungsaufgaben an.
b) Welche Arten von Zuordnungen liegen ihnen zugrunde?
2. a) Geben Sie verschiedene Lösungsverfahren für diese Aufgabe an.
b) Diskutieren Sie diese Verfahren im Hinblick auf den Unterricht.
3. Entwerfen Sie eine Unterrichtseinheit zur Behandlung folgender Aufgabe.
Ein Radfahrer und ein Auto fahren von A-Stadt nach B-Stadt. Der Radfahrer fährt um 10.27 Uhr ab mit einer durchschnittlichen Geschwindigkeit von
. Das Auto fährt um 11.12 Uhr ab mit einer durchschnittlichen Geschwindigkeit von
.
Um wieviel Uhr wird der Radfahrer vom Auto eingeholt?
4. Erläutern Sie, wie man anhand von Bewegungsaufgaben wichtige Aspekte des Funktionsbegriffs aufzeigen kann.
1982/II,3
Eine wichtige Darstellungsform positiver rationaler Zahlen sind Dezimalbrüche.
1. Erläutern Sie diese Darstellung.
2. a) Geben Sie Verfahren an, wie man Dezimalbrüche in gemeine Brüche und gemeine Brüche in Dezimalbrüche umwandeln kann.
b) Welche dieser Verfahren sind für die Hauptschule geeignet?
3. Wie lassen sich im Unterricht die Regeln für die Addition und Multiplikation von Dezimalbrüchen mit Hilfe der Regeln für das Rechnen mit gemeinen Brüchen erklären?
4. a) Erläutern Sie die Bedeutung der Dezimalbrüche für den Hauptschüler.
b) Diskutieren Sie Einsatzmöglichkeiten des Taschenrechners beim Arbeiten mit Dezimalbrüchen.
5. a) Geben Sie ein Kriterium dafür an, daß sich eine positive rationale Zahl als endlicher Dezimalbruch darstellen läßt (mit Begründung).
b) Man kann positive rationale Zahlen außer dem dekadischen System allgemein in g-adischen Systemen darstellen. Für welche Zahlen g lassen sich die Brüche
als endlicher g-adischer Bruch schreiben?
>> Zum Anfang
1982/I,1
1. a) Erläutern Sie die Begriffe "lineare Gleichung" und "Äquivalenzumformung einer linearen Gleichung".
b) Begründen Sie: "Die Addition einer reellen Zahl auf beiden Seiten einer Gleichung ist eine Äquivalenzumformung".
2. Welche Bedeutung hat die Behandlung der linearen Gleichung für die mathematische Ausbildung der Hauptschüler?
3. Skizzieren Sie eine Unterrichtsstunde, in der die Äquivalenzumformung einer linearen Gleichung eingeführt wird! Folgende Punkte sind dabei genauer zu behandeln
a) Diskussion des verwendeten Modells,
b) Lernzielsequenz,
c) Knappe Schilderung des geplanten Unterrichtsablaufs.
4. Wie sollen die in der Einführungsstunde angebahnten Erkenntnisse in den folgenden Stunden erweitert werden?
1982/I,2
1. Definieren Sie folgende Begriffe: "deckungsgleich", "zerlegungsgleich", "flächeninhaltsgleich". Geben Sie Beziehungen an, die zwischen diesen drei Begriffe bestehen.
2. Beschreiben Sie im einzelnen die Lernschritte, die vom Vergleichen über das Messen zum Berechnen des Inhalts von Rechtecksflächen führen!
3. Erläutern Sie die grundlegende Bedeutung der Inhaltsberechnung für das Rechteck für die Inhaltsbererechnung anderer Vierecksformen und des Dreiecks!
4. In welcher Weise lassen sich die mathematischen Fähigkeiten "Transformieren", "Ordnen" und "Argumentieren" im Zusammenhang mit der Flächenberechnung fördern?
1982/I,3
Das Sachrechnen im Mathematikunterricht der Hauptschule betrifft zum großen Teil Abbildungen von Größenbereichen auf sich selbst oder auf andere Größenbereiche.
1. Erklären Sie den Begriff Größenbereich und den Begriff Teilbarkeitseigenschaft in einem Größenbereich. Erläutern Sie beide Bergriffe am Beispiel der Längen und der Geldwerte!
2. Zeigen Sie, daß man (N;+;<) und Q+;+;<) als Größenbereiche interpretieren kann. Diskutieren Sie unter diesem Aspekt im Vor- und Nachteile der beiden folgenden Möglichkeiten für Zahlbereichserweiterung:
a) N ® ? ® Q, b) N ® Q+® Q.
3. Im Unterricht sind direkte und indirekte Proportionalitäten wichtige Abbildungen von Größenbereichen. Charakterisieren Sie beide Abbildungstypen! Geben Sie Beispiele für ihr Vorkommen aus dem Erfahrungsbereich der Schüler! Nennen Sie Darstellungsmöglichkeiten dieser Abbildungen!
4. Entwickeln und begründen Sie eine Folge von Übungsaufgaben, die der operativen Durcharbeitung der Proportionalitäten dient!
>> Zum Anfang
