|
... was ist das Ein anschauliches Beispiel für die Kugelgeometrie ist die Geometrie auf der Erdoberfläche, wenn wir die Erde näherungsweise als Kugel betrachten. Auf der Kugeloberfläche gibt es keine Geraden, aber ein Vielzahl unterschiedlicher Kreise.  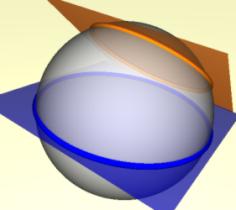
Schneiden wir die Kugel mit einer Ebene, die durch den Mittelpunkt der Kugel geht, so erhalten wir Großkreise. Auf der Erde sind die Längenkreise und der Äquator Großkreise. Schnittkreise, deren Schnittebene mit der Kugel nicht durch den Kugelmittelpunkt geht, heißen Kleinkreise. Satz: Auf der Kugeloberfläche ist die kürzeste Verbindung zweier Punkte das Stück eines Großkreises. Hilfssatz: Zeige zunächst anschaulich für die ebene Geometrie: Werden zwei Punkte A und B durch einen Kreisbogen verbunden, dann gilt: Je größer der Kreisradius, desto kürzer ist die Länge des Verbindungsbogens. Mit gedrückter Maustaste läßt sich der Punkt M verschieben. 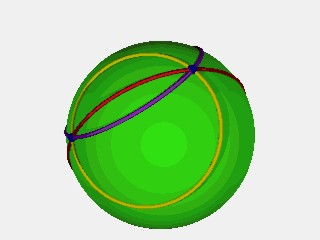 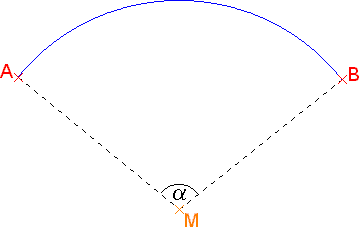 Welche Gemeinsamkeiten und welche Unterschiede gibt es zwischen der euklidischen Geometrie und der Kugelgeometrie? Hier kannst Du etwas über die Unterschiede erfahren. Hier kannst Du eine Auswahl der wichtigsten Definitionen und Sätze der Kugelgeometrie nachlesen. |