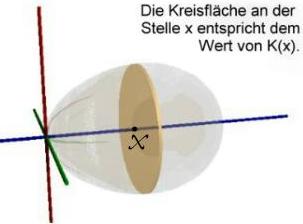
Integrationsanimation
Man kann also nun an jeder Stelle x zwischen -r und s dem Rotationskörper einen infinitesimalen dünnen Kreiszylinder einbeschreiben. Die Summe der infinitesimalen Zylindervolumina K(x)dx
ergeben das Volumen des Rotationskörpers.
Das nebenstehende
Bild zeigt solch einen infinitesimalen Zylinder.
Die dabei verwendete Kurve ist zwar genauer, doch wesentlich komplizierter.
Das Verfahren der Integration wird klarer, wenn man sich die Animation anschaut.
Führen wir die Integration aus:
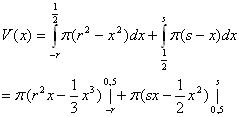
Nach Einsetzen der Grenzen erhält man ein Volumen von
![]()
Das Volumenproblem haben wir also analytisch gelöst. Während man das Eiervolumen auch leicht experimentell bestimmen kann, ist dies bei der Eieroberfläche nicht so einfach möglich. Vom analytischen Standpunkt aus ist aber fast genauso zu verfahren wie bei der Volumenintegration.
Hier gehts weiter zur
Oberflächenintegration.