Die Klothoide

Die Klothoide ist eine Kurve, deren Krümmung linear zu ihrer Bogenlänge zunimmt. In ihrem Nullpunkt besitzt sie also den Krümmungswert 0 und bildet von dort aus einen linksgekrümmten und einen rechtsgekrümmten Ast aus, deren Krümmung stetig zunimmt. Das Bildungsgesetz der Klothoide lautet

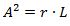
wobei A der sogenannte Klothoidenparameter ist, L die Bogenlänge der Klothoide vom Nullpunkt aus bezeichnet und r den Kehrwert der Krümmung (also den Radius des Schmiegkreises) im Endpunkt der Klothoide angibt.

In einem kartesischen Koordinatensystem ist die Klothoide definiert durch

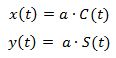
wobei

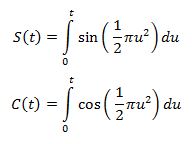
die sogenannten Fresnelintegrale darstellen und a als Streckfaktor fungiert.

Mit folgendem Geogebra-Applet lässt sich eine Klothoide zeichnen. Der Punkt "Integrationsgrenze" symbolisiert die Obergrenze t der Fresnelintegrale. Zieht man ihn nach rechts, erscheint der Punkt A, welcher die beiden Fresnelintegrale zum Zeitpunkt t als Koordinaten besitzt. Die Spur dieses Punktes liefert somit den linksgekrümmten Ast der Klothoide (erster Quadrant). Den rechtsgekrümmten Ast der Klothoide erzeugt das Applet durch Nullpunktspiegelung von A, wobei sich dieser auch wie der rechtsgekrümmte Ast elementar über die Fresnelintegrale zeichnen ließe. Über die Schieberegler im Applet lassen sich der Streckfaktor a sowie das Integrationsmaximum der Fresnelintegrale variieren. Durch letzteres bestimmt sich die Gesamtlänge der Klothoide.