
Das Differential
Nach
verschiedenen
Anläufen veröffentlicht Leibniz1684 seine
grundlegende Arbeit
zur Infinitesimalrechnung in den Acta eruditorum unter
dem Titel
Nova methodus pro
maximis et minimis, itemque tangentibus, quae nec fractas, nec
irrationales
quantitates moratur, et singulare pro illis calculi genus.
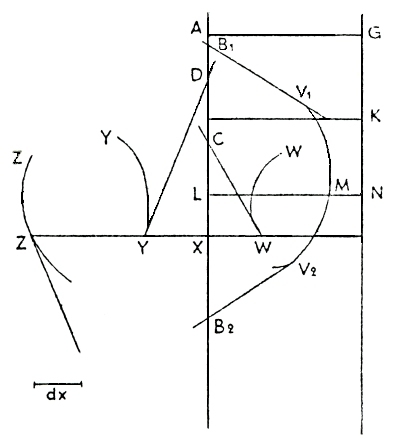
Die Arbeit war allerdings schwer zu verstehen. Schon die
überladene Figur macht es schwer, den zentralen Begriff des Differentials
(Leibniz spricht von differentia)
zu verstehen. Kowalewski hat die Figur zwar etwas
überarbeitet,
doch ist sie immer noch überladen. Reduziert man die Figur auf
die
Überlegungen zu einer
Kurve, dann versteht man, was Leibniz meint.
 |
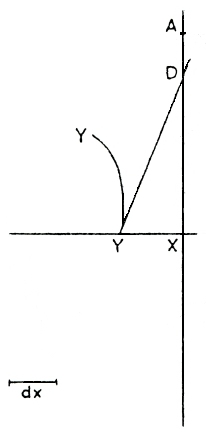 |
Leibniz betrachtet die Kurve YY mit der Tangente DY. Das charakteristische Dreieck DXY liefert mit dem Verhältnis
XY : DX die Tangentensteigung bezüglich der Achse AX. Er denkt sich schließlich eine beliebige Streckenlänge dx. Damit kann er nun das Differential dy definieren. dy ist diejenige Strecke, für die gilt:
dy : dx = XY : DX
(Tangentensteigung).
Schreibt man das
multiplikativ, dann gilt:
dy =
Tangentensteigung mal dx.
Heute definiert man
das Differential einer differenzierbaren Funktion y = f(x):
dy =
f'(x)dx.
Leibniz entwickelt den Kalkül der Differentiale: Er findet die Differentiale vieler Funktionen und auch die Summen-, Produkt- und Quotientenregel. Hier kommt dann Infinitesimales ins Spiel.
Das charakteristische Dreieck hatte er bei Blaise Pascal kennengelernt.

