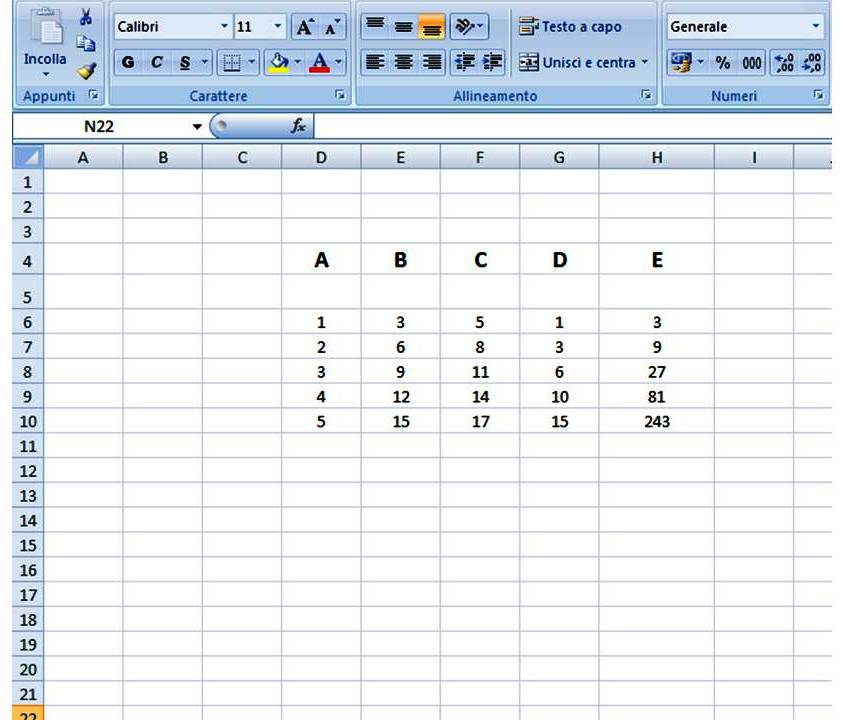
Alberta (A), Bruno (B), Carla (C), Dario (D), Elena (E) and Federico (F) are exploring the set of natural numbers and each one identifies a sequence. Here are the sequences identified:
A: 1, 2, 3, 4, 5, ..., ...
B: 3, 6, 9, 12, 15, ..., ...
C: 5, 8, 11, 14, 17, ..., ...
D: 1, 3, 6, 10, 15, ..., ...
E: 3, 9, 27, 81, 243, ..., ...
F: 2, 3, 5, 7, 11, ..., ...
The Problem
Activity 1
A worksheet is given to each student and an identical worksheet to the group. Every student analyses the situation individually and answers the questions mentally, possibly after having written on his sheet.
- What is, in your opinion, the sixth number that each of the six friends will take into account and how do you find it?
The students gather together in groups and discuss the solution, then they write it on the group worksheet.
- Tell the others how you answered the questions at the first point, then find a shared answer and write it on the worksheet.
- What is the tenth number in each sequence?
- And the fortieth? Explain how you find it.
- In your opinion, will someone among A, B, C, D, E, F, eventually find the number 1275 in his/her sequence? If yes, after how many steps?
- Justify your answer, by describing the approach you used.
- If you consider the number 2187, how would you answer the questions above?
- Can you find a natural number other than 0 that no one between A, B, C, D, E, F will ever take into account? Justify your answer.
- Is it possible to find at least one natural number that can never be reached by B or C or D or E or F? If yes, find such a number explaining the procedure. If not, explain why you think this number does not exist.
- Describe the characteristics of sequences A, B, C, D, E, F, so as to identify a rule (written in words) that can be used to determine any number of the sequence.
- Use your rule to calculate the seventieth and hundredth number of each sequence.
- Now use a letter, for example n, to indicate the n-th number of each sequence (the n-th number means the number occupying position n", where n can be any natural number). For each sequence, express with mathematical symbols a formula that represents the n-th number of the sequence.
You will have two options: (1) to write a "closed" formula that allows you to calculate, by using an expression that depends on n, the n-th number of the sequence; (2) write a "recursive" formula which expresses every number of the sequence as a function of the previous number (after defining explicitly the first number of the sequence). Try to list the advantages and the drawbacks of both formulas, if you find them both. For example, to describe the sequence of even numbers, we may write E(n) = 2n as a closed formula, and E(n+1) = E(n)+2 as a recursive formula, giving that E(0) = 0, where E states for even.
Activity 2
A worksheet is given to each student and an identical worksheet to the group. Every student individually analyses the situation and mentally answers to questions, possibly after having written on his/her sheet. The students come together, discuss the solution and then write it on the common worksheet.
- Gabriella says: "All the numbers of the formula
n^2-n+41belong to the set of numbers considered by F!" Do you think Gabriella is right? Why? Justify your answers.
- Ilario says: "The numbers considered by A are more than the ones considered by each of the other five friends!" and also: "Both B and C consider more numbers than those that may be considered by D, E and F". Do you think Ilario is right? Why? Justify your answers.
Activity 3
Two worksheets are given to every student (the first to invent a problem, the second to solve a problem invented by other students). Every student thinks individually and writes on the first worksheet. Later he/she uses the second sheet to answer a question posed by another student. To carry out this activity on-line a discussion forum can be a suitable tool.
- Invent a rule that allows you to build a sequence of natural numbers and write it down on the sheet.
- Now show to your schoolmates the first five elements of your sequence, asking them to use them to find out the rule you have written.
- Select a sequence among those posed by your peers and solve it on the second sheet.