Schüler begegnen Daten und Statistiken in den verschiedensten Situationen im Alltag, sei es in den Nachrichten, in der Werbung oder später im Berufsleben oder an der Universität. Deshalb ist es wichtig, dass sich Schüler einerseits Kompetenzen aneignen, um Statistiken interpretieren zu können und darauf aufbauend vernünftige Urteile fällen können, andererseits müssen Schüler Statistiken nutzen können, um ihre Argumente zu untermauern und zu rechtfertigen. Zahlreiche Datendarstellungen können dafür genutzt werden. Eine Vielzahl an Darstellungsformen bietet eine gute Möglichkeit Verbindungen zwischen den Darstellungen, welche den Schülern offensichtlich sind, herzustellen und die verschiedenen Mittelpunkte und Absichten zu beleuchten, welche die Nutzung empfehlenswert macht, wenn man sich mit Daten und Statistik im Unterricht beschäftigt.
Der größte Vorteil einer ICT Nutzung im Bereich Daten und Statistik ist die um einiges vereinfachte Kreation von anspruchsvollen Datendarstellungen, die entweder per Hand eingetippt oder sogar automatisch durch eine mathematische oder phsikalische Software erfasst wurden. ICT ermöglicht außerdem den Lehrern und Schülern Parameter mühelos zu verändern und die Veränderungen, welche die Variation in den Ergebnissen verursacht, dynamisch zu beobachten.
Absolute und relative Häufigkeit
Für ein Ereignis i ist die absolute Häufigkeit ni die Anzahl wie oft das Ereignis in einem Zufallsexperiment vorkommt. Die relative Häufigkeit ist definiert als der Quotient der absolute Häufigkeit und der Anzahl der Ereignisse N des Experiments:
Eine Verkehrszählung
Unsere Tabelle erfasst alle Fahrräder, die in einem gegebenen Zeitabstand gezählt wurden. Die grünen Zahlen enstprechen der relativen Häufigkeit der gezählten Fahrräder an einem Tag.
| Uhrzeit | Mo | Di | Mi |
| 00 - 8 | 16 \frac{16}{37} \approx 43\% |
22 \frac{22}{44} = 50\% |
31 \frac{31}{69} \approx 45\% |
| 8 - 16 | 20 \frac{20}{37} \approx 54\% |
20 \frac{20}{44} \approx 45\% |
34 \frac{31}{69} \approx 49\% |
| 16 - 00 | 1 \frac{1}{37} \approx 3\% |
2 \frac{2}{44} \approx 5\% |
4 \frac{4}{69} \approx 6\% |
| Summe | 37 | 44 | 69 |
Piktogramm und Säulendiagramm
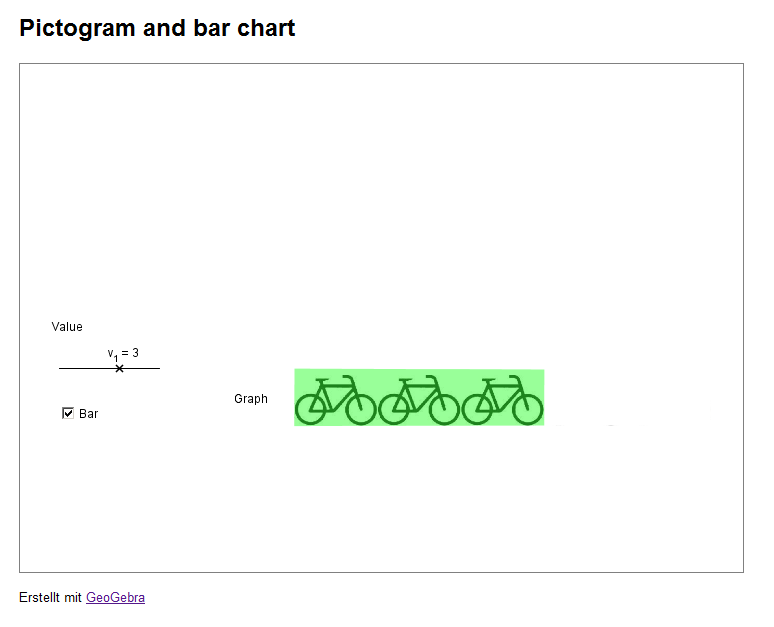
Eine Möglichkeit eines Graphens ist ein Piktogramm. Ein Piktogramm nutzt Symbole/Zeichen um Daten darzustellen.
Beispiel:
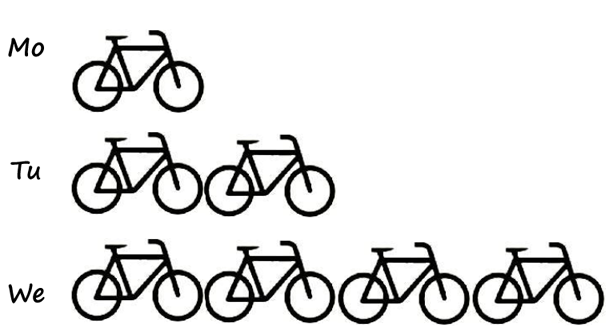
In diesem sehr kurzen Beispiel siehst du ein Piktogramm der gezählten Fahrräder an einem Ort innerhalb eines bestimmten Zeitintervals.
| Tabelle | Graphen | ||||||||||
|
|
Das Applet rechts zeigt wie man aus einem Piktogramm ein Säulendiagramm erstellt.
Grundlegende Schlüsselfiguren
Für eine gegebene Folge von Ereignissen \left\{ x_1, x_2, ..., x_n \right\} sind folgende Schlüsselfiguren einige der grundlegensten der deskritpiven Statistik:
- Arithmetisches Mittel
Das aritmetische Mittel ist definiert als der Quotient der Summe aller Werte geteilt durch die Anzahl der Werte: \overline{x} = \frac{1}{n} \sum_{i=1}^n x_i - Streuung
Die Streuung ist definiert als die Differenz zwischen dem kleinsten und dem größten Wert aus der Stichprobe. - Wert des Medians
Der Wert des Medians ist als numerischer Wert definiert, der die Stichprobe in zwei gleich große Teilmengen teilt, so dass jeder Wert einer Teilmenge kleiner als der Wert des Medians ist und jeder Wert einer anderen Teilmenge größer oder gleich dem Wert des Medians ist.
Beispiel:
In dieser Tabelle finden wir die oben genannten Größen in Verbindung mit dem Alter von einigen Spielern der spanischen Fussballmannschaft, die 2010 die Weltmeisterschaft gewonnen haben:
| Tabelle | Schlüssefiguren | |||||||||||||||||||||||
|
|
Tortendiagram und vertikales Säulendiagramm
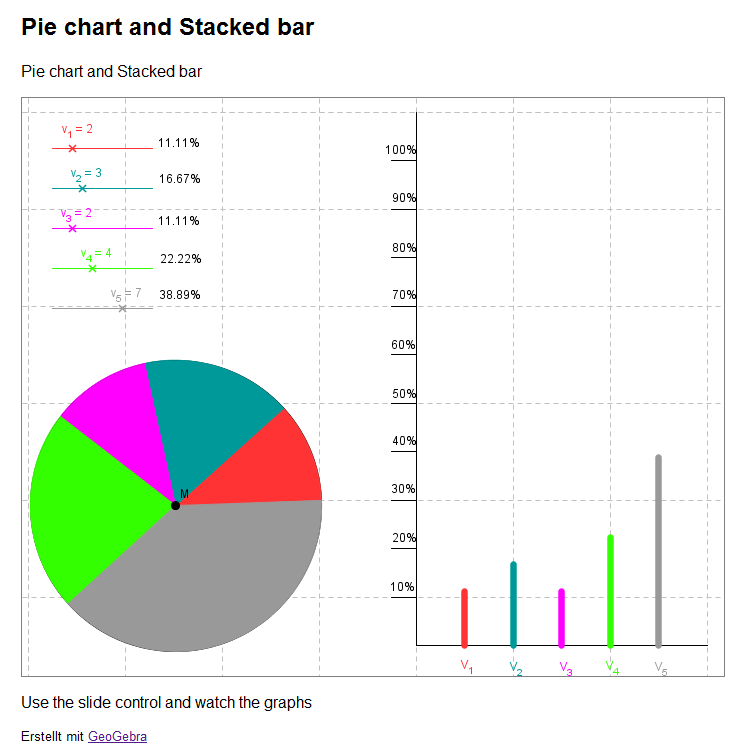
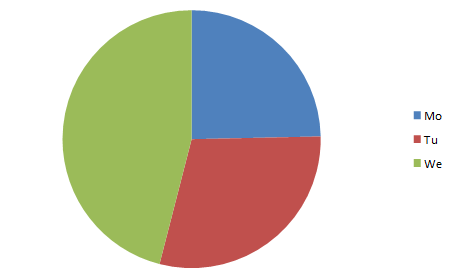
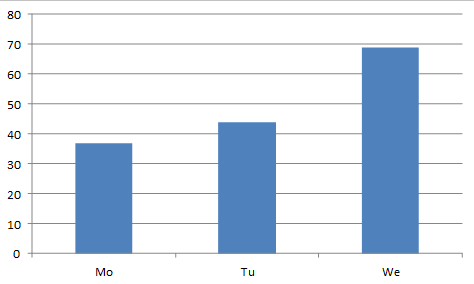
In einem Säulendiagramm können die absolute und die relative Häufigkeit einer Datenstichprobe dargestellt werden. Die Säulen können vertikal oder horizontal gezeichnet werden. Ein Tortendiagramm stellt immer die relative Häufigkeit einer Stichprobe dar.
Beispiel:
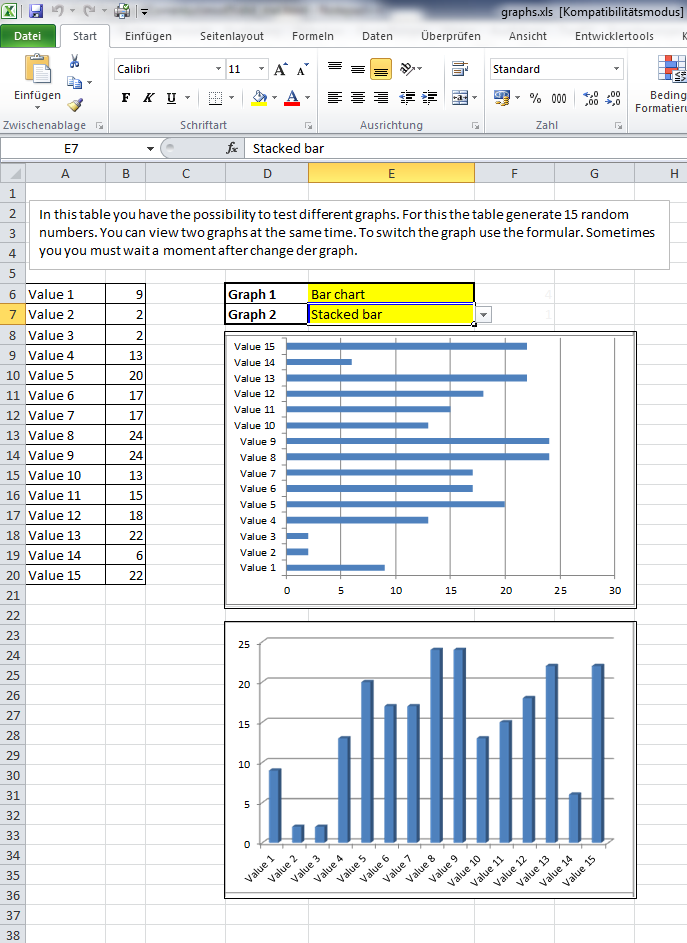
Eine Verkehrszählung wurde an einem bestimmten Ort durchgeführt. Wir wollen die Ergebnisse graphisch darstellen:
| Tabelle | Graphen | ||||||||||
|
|
Beachte: Die Datei funktioniert nur mit Microsoft Office Excel 2007 und 2010, da Open Office und ältere Versionen von Excel diese Funktionen nicht unterstützen.
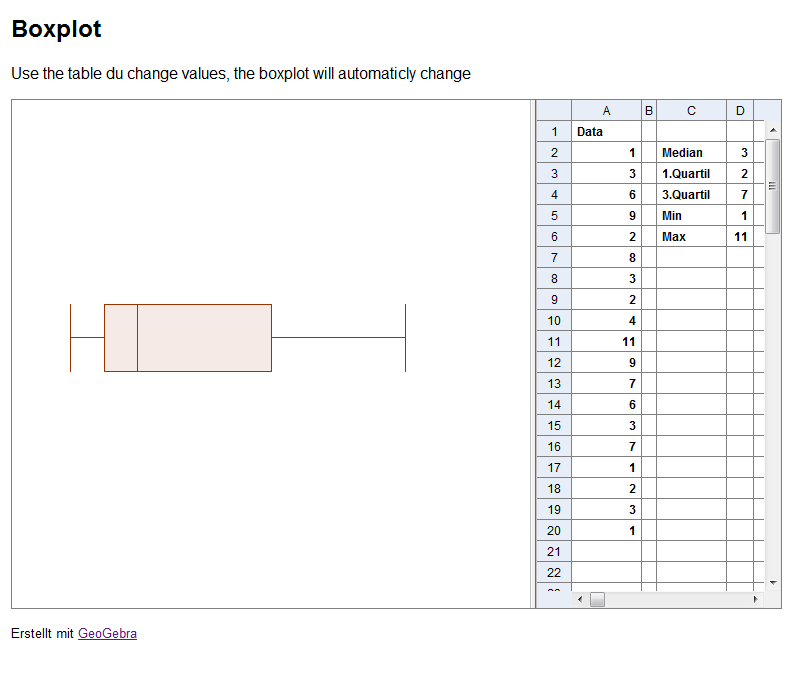
Boxplot
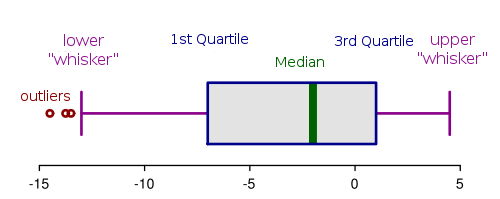 Ein weiterer wichtiger Graph nennt sich "Boxplot". Dieser stellt eine Anzahl von wichtigen Zahlen in einer klaren Darstellung dar. Du kennst bereits den minimalen und den maximalen Wert und auch den Wert des Medians.
Ein weiterer wichtiger Graph nennt sich "Boxplot". Dieser stellt eine Anzahl von wichtigen Zahlen in einer klaren Darstellung dar. Du kennst bereits den minimalen und den maximalen Wert und auch den Wert des Medians.
Teile den Median für eine Stichprobe in zwei Hälften,
- das 1. Quartil ist der Median der unteren Hälfte der Daten
- das 3. Quartil ist der Median der oberen Hälfte der Daten.
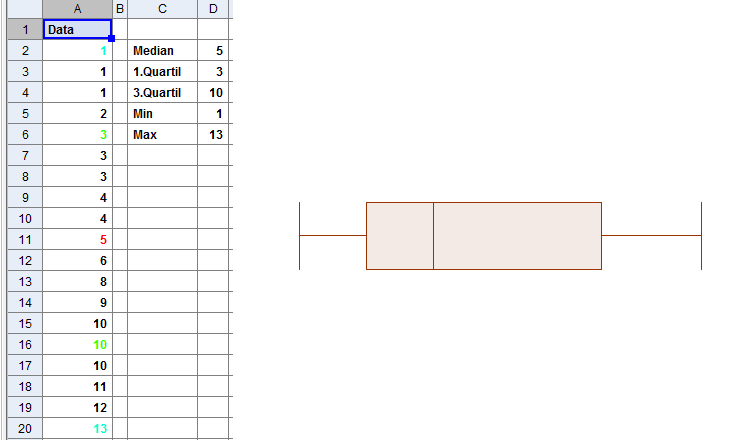
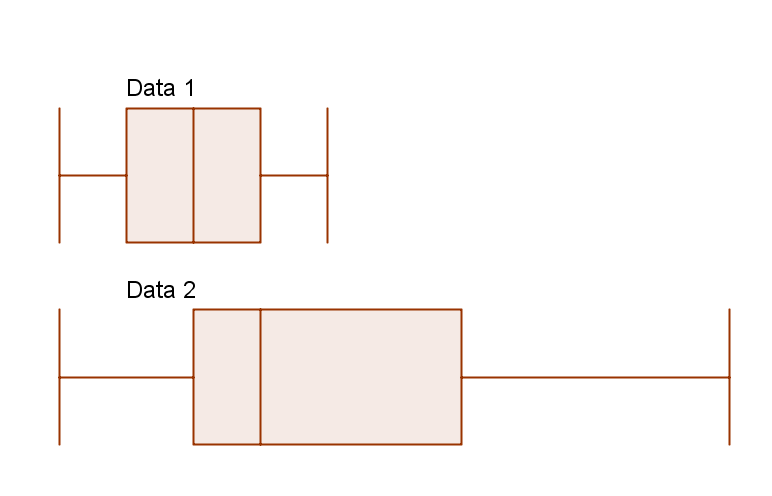
Ein Boxplot stellt den Bereich der Werte zwischen dem ersten und dem dritten Quartil als Box dar, welche eine Linie beinhaltet die den Median anzeigt. Die so genannten "Whisker" an beiden Enden der Box legen die minmalen und maximalen Werte dar. Manchmal werden beim Boxplot Ausreißer durch abgelegene Punkte dargestellt.
Das Originalbild des Boxplots wurde durch den Nutzer RobSeb via Wikimedia Commons mit der Lizenz CC-BY-SA zur Verfügung gestellt.
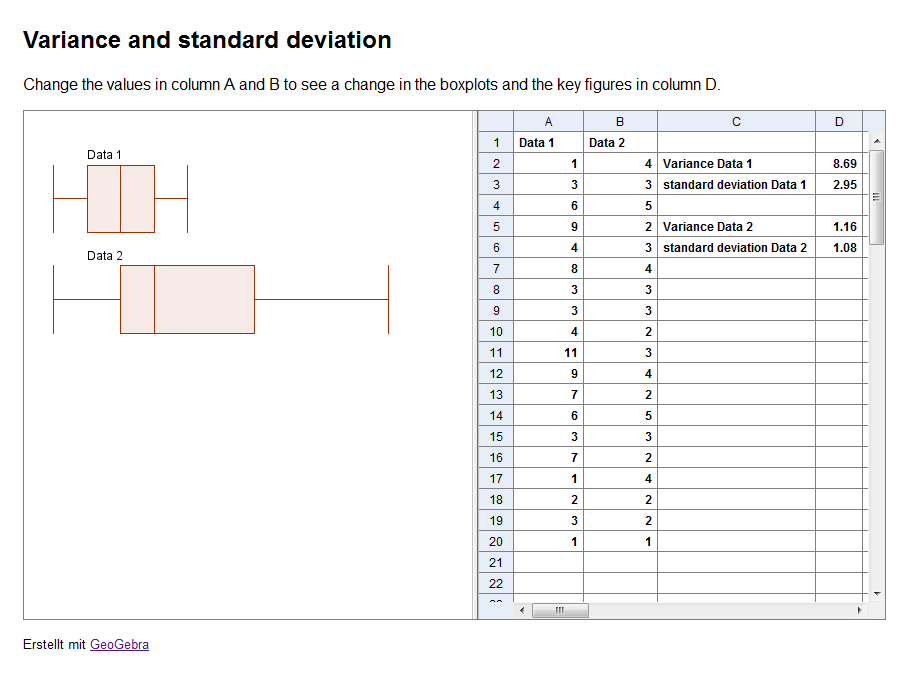
Varianz und Standardabweichung
Zu guter Letzt gibt es noch zwei weitere Schlüsselfiguren: die Varianz und die Standardabweichung, welche die statistische Streuung der Stichprobe messen.
- Varianz
Die Varianz s2 ist, in einer Population an Stichproben, der Mittelwert der quadratischen Abweichung zwischen den betreffenden Stichproben und deren Mittelwert:s^2 = \frac{1}{n} \sum_{i=1}^n (x_i - \overline x)^2 - Standardabweichung
Die Standardabweicung ist die Wurzel der Varianz: