Wachstum ist im Mathematikunterricht für mathematische Konzeptformationen und für schwere Anwendungsaufgaben ein ergiebiges Thema. Wachstumsprozesse können in vielen Gebieten des wirklichen Lebens gefunden werden. Dazu zählt unter anderem die Biologie, die Physik oder das Finanzwesen. Da Folgen ein grundlegender Bestandteil des Mathematikunterrichts sind, können Wachstumsfolgen innerhalb jeder Klassenstufe der Schule auf verschiedenen Schwierigkeitsgraden angesprochen werden. Lineare Folgen, Polynomfolgen oder exponentielle Folgen sind die gängigen Beispiele. Man könnte sich auch mit dem logistischen Wachstum, das in der Realität gebräuchlichste Wachstum, beschäftigen. Außerdem gibt es zahlreiche Möglichkeiten Wachstumgsfolgen darzustellten, z.B. durch (diskrete) Graphen, Wertetabellen und explizite oder rekursive Gleichungen, was eine gute Möglichkeit liefert Kompetenzen der mathmatischen Darstellungsfähigkeiten zu fördern.
Diese verschiedenen Darstellungsmöglichkeiten machen die Nutzung des ICT besonders ergiebig, da man Darstellungen dynamisch verknüpfen kann, um Verbindungen auf zu zeigen und um sie interaktiv variabel zu gestalten. Es gibt verschiedene Programme, die Möglichkeiten anbieten, Wachstumsfolgen darzustellen, d.h. mathematische Lernprogramme wie Geogebra, Handgeräte oder eine Software für Tabellenkalkulationsprogramme. Ein bemerkenswerter Vorteil einer Software für ein Tabellenkalkulationsprogramm ist die Art, wie die diskreten Softwarezellen eng mit den Termen der Folge zusammenhängen und die relative Einfachheit eine Wertetabelle zu erstellen, in dem rekursive Formeln genutzt werden, was im Anschluss in Graphen oder Diagrammen dargestellt werden kann.
Lineares Wachstum
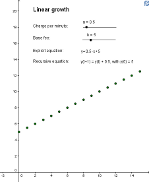
Wenn der Wachstumsprozess von einem Schritt zum nächsten (ein Schritt kann ein Tag, ein Monat oder ein Jahr sein) beschrieben wird, sind rekursiv definierte Folgen ein gutes mathematisches Modell. Wenn die Differenz von zwei direkt aufeinanderfolgenden Termen der Folge konstant ist, dann sprechen wir von linearem Wachstum.
Allgemein:
| Gleichung | Wertetabelle | Graph | |||||||||||||||||||||
|
f(n+1) = a + f(n) mit f(0) = b oder f(n) = a \cdot n + b |
|
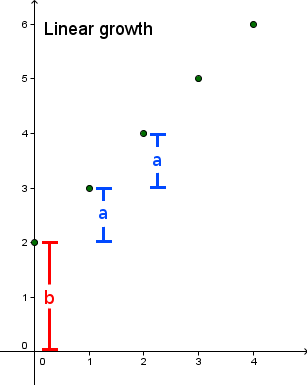
|
Beispiel:
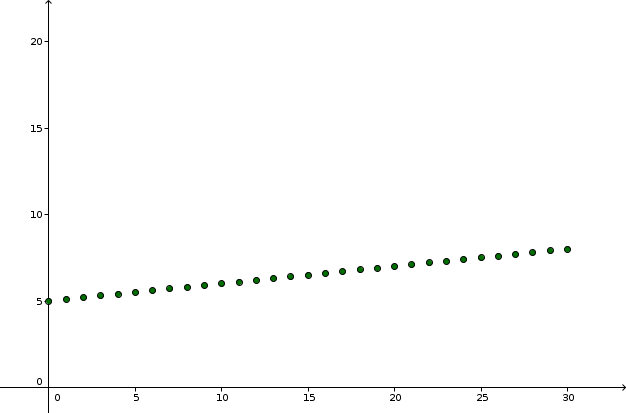
Ein Handyanbieter verlangt 10 Cent pro Minute mit einem festen Grundpreis von 5 € im Monat. Sei t die Anzahl der Minuten, die in einem bestimmten Monat telefoniert werden. Die Kosten c(t) können als (rekursive oder explizite) Gleichung, als Wertetabelle oder als Graph mit einer linearen Wachstumsfolge visualisiert werden:
| Gleichung | Wertetabelle | Graph | |||||||||||||||||||||
|
c(t+1) = 0.1 + c(t) mit c(0) = 5 oder c(t) = 0.1 \cdot t + 5 |
|
|
Exponentielles Wachstum
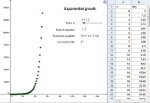
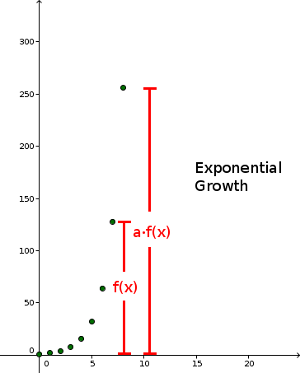
Wenn der Quotient von zwei direkt aufeinanderfolgenden Termen der Folge konstant ist, dann sprechen wir von exponentiellem Wachstum. Mit anderen Worten: werden die direkt vorherigen Terme mit einer festen Konstanten multipliziert, ist das Ergebnis ein Term der Folge. Dies gilt für die gesamte Folge.
| Gleichung | Wertetabelle | Graph | |||||||||||||||||||||
|
f(n+1) = a \cdot f(n) mit f(0) = 1 oder f(n) = a^n |
|
|
Beispiel:
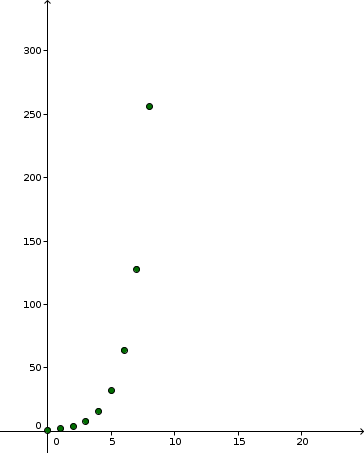
Wenn Bakterienkolonien genügend Raum und Nahrung gegeben wird, dann verdoppeln diese ihre Anzahl durch binäre Zellspaltung innerhalb jedes Schrittes ihrer Reproduktion. Sei b(t) die Anzahl der Bakterien nach t Schritten. Für eine Bakterie kann die dargestellte Wachstumsfolge wie folge dargestellt werden:
| Gleichung | Wertetabelle | Graph | |||||||||||||||||||||
|
b(t+1) = 2 \cdot b(t) mit b(0) = 1 oder b(t) = 2^t |
|
|
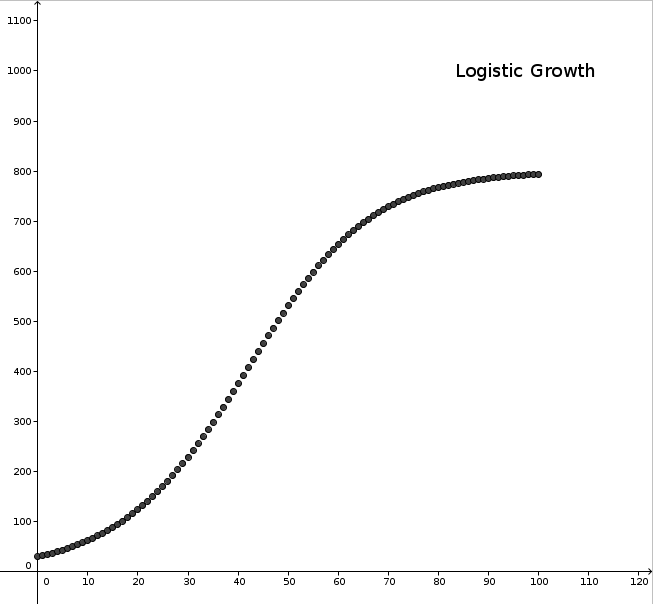
Logistisches Wachstum ist ein realistisches Modell des Bevölkerungswachstums, das für jede Art von Population genutzt werden kann deren Wachstumsmöglichkeiten eingeschränkt sind. Anfangs ist es, mit der realistischen Vermutung einer zwanghaften maximalen Bevölkerungsgröße, dem exponentiellem Wachstum sehr ähnlich.
Das logistische Wachstum ist durch den Anstieg oder die Senkung \Delta f(x) einer Folge definiert, was proportional ist zu
- der momentaten Bevölkerungszahl
- der Differenz der maximalen und der momentanen Bevölkerungszahl (G-f(x))
- der Reproduktions- und Hungersrate der Bevölkerung, die sich aus der Konstanten k ergibt
Wenn wir den Schritt von x nach x+1 machen, was in einem Anstieg von f(x) auf f(x+1) resultiert, erhalten wir:
oder \Delta f(x) = k \cdot f(x) \cdot (G-f(x)),
mit einer Konstanten k. Dies resultiert in der unten stehenden Gleichung: