Kartesisches Koordinatensystem
Das kartesische Koordinatensystem ist ein rechtwinkliges Koordinatensystem, das jeden Punkt in der Ebene mit
einem Paar von Zahlen verbindet und umgekehrt. Es wird durch zwei senkrechte Linien, die sich im Ursprung der
Ebene schneiden, identifiziert.
Die Position eines Punktes P auf der kartesischen Ebene wird dann unter Verwendung eines geordneten
Paars von reellen Zahlen beschrieben: (x, y). Die erste Zahl x gibt die horizontale Position des Punktes
vom Ursprung an, während die zweite Zahl y, die vertikale Position darstellt. Die beiden Zahlen sind
jeweils x-und y-Koordinate des Punktes P.
Geometrie
Zum Beispiel, für den Punkt (3,4) ist die x-Koordinate gleich 3 und die y-Koordinate gleich 4.
Abstand
Der Abstand d von P (x, y) bis Q (u, v) wird durch die Formel definiert:
Manchmal wird der Abstand von P zu Q als d (P, Q) angegeben.
Der Abstand d von P (x, y) bis Q (u, v) wird durch die Formel definiert:
d=\sqrt{(u-x)^2+(v-y)^2}.
Manchmal wird der Abstand von P zu Q als d (P, Q) angegeben.
Zum Beispiel ist der Abstand zwischen A (2,3) und B (5,7) folgender:
d=\sqrt{(5-2)^2+(7-3)^2}=\sqrt{9+16}=\sqrt{25}=5.
Satz des Pythagoras
Der Satz des Pythagoras ist einer der fundamentalen Sätze der euklidischen Geometrie. Er besagt, dass in allen ebenen, rechtwinkligen Dreiecken die Summe der Flächeninhalte der Quadrate über den Katheten gleich dem Flächeninhalt des Quadrates über der Hypotenuse ist.
Der Satz des Pythagoras ist einer der fundamentalen Sätze der euklidischen Geometrie. Er besagt, dass in allen ebenen, rechtwinkligen Dreiecken die Summe der Flächeninhalte der Quadrate über den Katheten gleich dem Flächeninhalt des Quadrates über der Hypotenuse ist.
Funktion
Eine Funktion ordnet jedem Element einer Menge (das Argument der Funktion oder der Eingang) ein Element der anderen Menge (der Wert oder die Ausgabe) zu. Das Argument und der zugehörige Wert können Elemente aus jeder beliebigen Menge sein. Die beiden Mengen werden als Definitionsbereich und Wertebereich der Funktion bezeichnet. Wenn der Definitionsbereich und der Wertebereich aus den reellen Zahlen sind, ist die Funktion eine reelle Funktion mit reellen Variablen. Normalerweise ist die Notation für eine Funktion für die reelle Zahl x folgende:
Eine Funktion ordnet jedem Element einer Menge (das Argument der Funktion oder der Eingang) ein Element der anderen Menge (der Wert oder die Ausgabe) zu. Das Argument und der zugehörige Wert können Elemente aus jeder beliebigen Menge sein. Die beiden Mengen werden als Definitionsbereich und Wertebereich der Funktion bezeichnet. Wenn der Definitionsbereich und der Wertebereich aus den reellen Zahlen sind, ist die Funktion eine reelle Funktion mit reellen Variablen. Normalerweise ist die Notation für eine Funktion für die reelle Zahl x folgende:
f(x).
In diesem Fall stammt das Element x aus dem Definitionsbereich X und f (x) aus dem Wertebereich Y (f, sodass: X -> Y).
Wenn y ein Element von Y ist, folgt daraus:
y = f(x).
f (x) wird auch als das Bild von x unter der Funktion f bezeichnet.
Ein Beispiel für eine reelle Funktion ist:
f(x) = 2x + 1,
auf dessen Grundlage wird jedem Wert x der entsprechende Wert durch den Ausdruck 2x + 1 zugeordnet.
Es gibt viele Möglichkeiten, um Funktionen zu beschreiben oder zu repräsentieren: durch eine Formel,
durch einen Algorithmus, welcher sie berechnet, durch einen Tabelle oder durch einen Graphen.
Der Graph einer Funktion ist die Menge aller geordneten Paare (x, f (x)), für alle x im Definitionsbereich X. Wenn die Funktion real ist, kann die Menge seiner geordneten Paare in ein kartesisches Koordinatensystem übertragen werden, wobei die geordneten Paare die Koordinaten in der Ebene sind.
Der Graph einer Funktion ist die Menge aller geordneten Paare (x, f (x)), für alle x im Definitionsbereich X. Wenn die Funktion real ist, kann die Menge seiner geordneten Paare in ein kartesisches Koordinatensystem übertragen werden, wobei die geordneten Paare die Koordinaten in der Ebene sind.
Modell
Funktionen werden oft als Modelle von Situationen verwendet.
Funktionen werden oft als Modelle von Situationen verwendet.
Zum Beispiel kann die gleichförmige Bewegung durch eine lineare Funktionen modelliert werden f (x) = mx + q.
Mathematische Modelle werden für viele Anwendungen genutzt, nicht nur in den Naturwissenschaften, wie Physik,
Biologie, Geowissenschaften, Meteorologie usw., sondern auch in den Sozialwissenschaften, wie Ökonomie und Psychologie.
Kegelschnitte
In der analytischen Geometrie repräsentiert ein Kegelschnitt eine algebraische Kurve zweiten Grades. Es ist ein Ort von Punkten, deren Abstände in einem festen Verhältnis zu bestimmten Punkt(en) stehen. In der euklidischen Geometrie gibt es drei Haupttypen von Kegelschnitten: die Ellipse, Parabel und Hyperbel. Der Kreis kann als vierter Typ oder als speziellen Fall der Ellipse gesehen werden. Unterschiedliche Gleichungen werden mit den verschiedenen Kegelschnitten verbunden.
In der analytischen Geometrie repräsentiert ein Kegelschnitt eine algebraische Kurve zweiten Grades. Es ist ein Ort von Punkten, deren Abstände in einem festen Verhältnis zu bestimmten Punkt(en) stehen. In der euklidischen Geometrie gibt es drei Haupttypen von Kegelschnitten: die Ellipse, Parabel und Hyperbel. Der Kreis kann als vierter Typ oder als speziellen Fall der Ellipse gesehen werden. Unterschiedliche Gleichungen werden mit den verschiedenen Kegelschnitten verbunden.
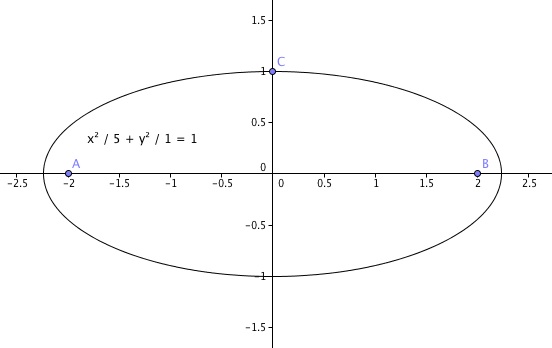
Ellipse
Die kanonische Gleichung zweiten Grades einer Ellipse hat die folgende Form:
Die kanonische Gleichung zweiten Grades einer Ellipse hat die folgende Form:
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
where a and b give respectively the major and minor semi-axes, that is the two halves of the major and minor diameters of the ellipse.
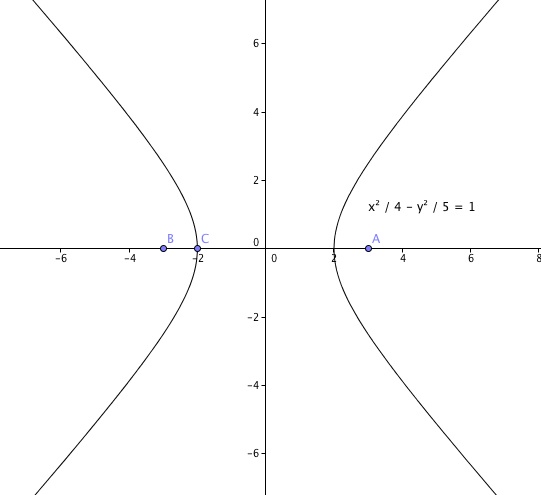
Hyperbel
Die kanonische Gleichung zweiten Grades einer Hyperbel hat die Form:
Die kanonische Gleichung zweiten Grades einer Hyperbel hat die Form:
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1
wo wieder a und b die großen bzw. kleinen Halbachsen der Hyperbel darstellen.
Trigonometrische Funktionen
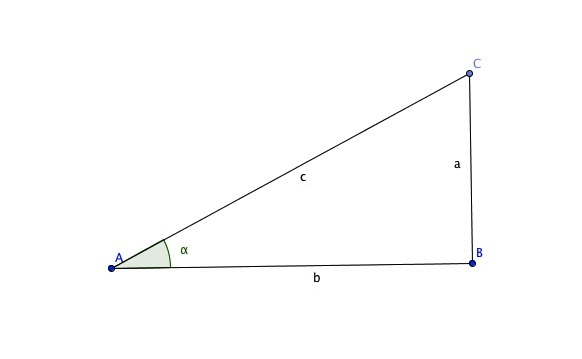
In der Trigonometrie, wo es um die Beziehungen zwischen den Seiten und Winkel eines Dreiecks geht, werden die trigonometrischen Funktionen definiert, die Beziehungen in Bezug auf zyklische Phänomene (wie Wellen) beschreiben. Die trigonometrischen Funktionen werden unter Verwendung der Seitenlängen eines rechtwinkligen Dreiecks (a, b (die Schenkel) und c (die Hypotenuse)) und der gegebenen Winkel (alpha ist definiert als der Winkel gegenüber a) definiert.
In der Trigonometrie, wo es um die Beziehungen zwischen den Seiten und Winkel eines Dreiecks geht, werden die trigonometrischen Funktionen definiert, die Beziehungen in Bezug auf zyklische Phänomene (wie Wellen) beschreiben. Die trigonometrischen Funktionen werden unter Verwendung der Seitenlängen eines rechtwinkligen Dreiecks (a, b (die Schenkel) und c (die Hypotenuse)) und der gegebenen Winkel (alpha ist definiert als der Winkel gegenüber a) definiert.
Sinus
Sinus-Funktion (sin) ist das Verhältnis der Seite gegenüber dem Winkel (a) zur Hypotenuse (c):
Sinus-Funktion (sin) ist das Verhältnis der Seite gegenüber dem Winkel (a) zur Hypotenuse (c):
\sin \alpha = \frac{a}{c}
Cosinus
Cosinus-Funktion (cos) ist das Verhältnis der benachbarten Seiten b und c: Schenkel (b) zur Hypotenuse (c):
Cosinus-Funktion (cos) ist das Verhältnis der benachbarten Seiten b und c: Schenkel (b) zur Hypotenuse (c):
\cos \alpha = \frac{b}{c}
Die Tangens-Funktion ist definiert als Verhältnis des gegenüberliegenden Schenkels a und des anliegenden
Schenkel b oder als Verhältnis von sin (alpha) zu cos (alpha).Die Kehrwerte dieser Funktionen werden als
Kosekants-, Sekans- und Kotangensfunktion bezeichnet.